题目内容
已知椭圆C的对称中心为原点O,焦点在x轴上,离心率为
,且点(1,
)在该椭圆上.
(1)求椭圆C的方程;
(2)过椭圆C的左焦点F1的直线l与椭圆C相交于A、B两点,若△AOB的面积为
,求直线l的方程.
| 1 |
| 2 |
| 3 |
| 2 |
(1)求椭圆C的方程;
(2)过椭圆C的左焦点F1的直线l与椭圆C相交于A、B两点,若△AOB的面积为
6
| ||
| 7 |
考点:直线与圆锥曲线的综合问题
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)设出椭圆方程,由离心率公式,以及a,b,c的关系,和已知点代入方程,求出a,b即可;
(2)求出左焦点坐标,设出直线l的方程,注意斜率不存在的情况,将直线方程与椭圆方程联立消去y,得到关于x的二次方程,运用韦达定理,再用弦长公式,求出原点到直线的距离,运用面积公式,列出方程,然后求出k2,即可得到l的方程.
(2)求出左焦点坐标,设出直线l的方程,注意斜率不存在的情况,将直线方程与椭圆方程联立消去y,得到关于x的二次方程,运用韦达定理,再用弦长公式,求出原点到直线的距离,运用面积公式,列出方程,然后求出k2,即可得到l的方程.
解答:
解:(1)设椭圆方程为
+
=1,
又e=
=
,a2-b2=c2,
+
=1,
解得,a=2,b=
,
∴椭圆C的方程为
+
=1;
(2)由于F1(-1,0),设直线l的方程为x=-1或y=k(x+1),
若l;x=-1,则AB=
=3,△ABO的面积为
,不成立;
若l:y=k(x+1),将其代入椭圆方程,得到(3+4k2)x2+8k2x+4k2-12=0
∴x1+x2=
,x1x2=
∴AB=
=
•
又O到直线l的距离为
,
∴S△AOB=
•
•
=
,
解得k2=1,即k=±1,
∴直线l的方程为:y=±(x+1).
| x2 |
| a2 |
| y2 |
| b2 |
又e=
| c |
| a |
| 1 |
| 2 |
| 1 |
| a2 |
| ||
| b2 |
解得,a=2,b=
| 3 |
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)由于F1(-1,0),设直线l的方程为x=-1或y=k(x+1),
若l;x=-1,则AB=
| 2×3 |
| 2 |
| 3 |
| 2 |
若l:y=k(x+1),将其代入椭圆方程,得到(3+4k2)x2+8k2x+4k2-12=0
∴x1+x2=
| -8k2 |
| 3+4k2 |
| 4k2-12 |
| 3+4k2 |
∴AB=
| 1+k2 |
|
| 1+k2 |
12
| ||
| 3+4k2 |
又O到直线l的距离为
| |k| | ||
|
∴S△AOB=
| 1 |
| 2 |
| |k| | ||
|
| 12(1+k2) |
| 3+4k2 |
6
| ||
| 7 |
解得k2=1,即k=±1,
∴直线l的方程为:y=±(x+1).
点评:本题主要考查椭圆的方程和几何性质,考查直线与椭圆的位置关系,以及弦长公式,考查运算能力.

练习册系列答案
相关题目
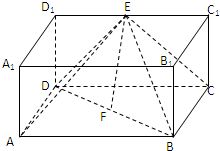 在长方体ABCD-A1B1C1D1中,DC=2DD1,E,F分别为棱C1D1,BD的中点.
在长方体ABCD-A1B1C1D1中,DC=2DD1,E,F分别为棱C1D1,BD的中点. 如图所示,在三棱柱ABC-A1B1C1中,M、N分别是BC和A1B1的中点.
如图所示,在三棱柱ABC-A1B1C1中,M、N分别是BC和A1B1的中点.