题目内容
当a=
dx时,二项式(x2-
)6展开式中的x3的系数为 .
| 2 |
| π |
| ∫ | 2 0 |
| 4-x2 |
| a |
| x |
考点:二项式系数的性质
专题:二项式定理
分析:利用定积分求出a,然后利用二项式定理求解展开式中的x3的系数.
解答:
解:a=
dx,
dx的几何意义是以原点为圆心半径为2的
的圆的面积,
∴a=
×
π×22=2.
二项式(x2-
)6=(x2-
)6,展开式的通项公式为:
x12-2r•(-2)r•x-r=
x12-3r•(-2)r,
令12-3r=3,则r=3.
二项式(x2-
)6展开式中的x3的系数为:
(-2)3=-160.
故答案为:-160.
| 2 |
| π |
| ∫ | 2 0 |
| 4-x2 |
| ∫ | 2 0 |
| 4-x2 |
| 1 |
| 4 |
∴a=
| 2 |
| π |
| 1 |
| 4 |
二项式(x2-
| a |
| x |
| 2 |
| x |
| C | r 6 |
| C | r 6 |
令12-3r=3,则r=3.
二项式(x2-
| a |
| x |
| C | 3 6 |
故答案为:-160.
点评:本题考查二项式定理与微积分基本定理,着重考查二项展开式的通项公式,考查理解与运算的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
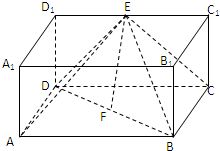 在长方体ABCD-A1B1C1D1中,DC=2DD1,E,F分别为棱C1D1,BD的中点.
在长方体ABCD-A1B1C1D1中,DC=2DD1,E,F分别为棱C1D1,BD的中点. 如图所示,在三棱柱ABC-A1B1C1中,M、N分别是BC和A1B1的中点.
如图所示,在三棱柱ABC-A1B1C1中,M、N分别是BC和A1B1的中点. 某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.则样本的平均值是
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.则样本的平均值是