题目内容
在2014-2015赛季的CBA(中国职业篮球)常规赛中,甲、乙两队要进行三场比赛,在三场比赛中,甲队两个主场一个客场,乙队一个主场两个客场,按以往多年的比赛统计,两队主客场的胜负概率如下表,按照比赛规定,每场胜队得2分,负队得1分(比赛结果只有胜负两种可能,如果出现平局时就加时,直至分出胜负为止),设甲、乙两队最后所得的总分分别为ξ、η,且ξ+η=9.
(1)甲队得5分的概率;
(2)求ξ的分布列,并用统计学知识说明两个队的实力情况.
| 主客场 | 甲队胜 | 乙队胜 | ||||
| 甲对主场 |
|
| ||||
| 乙队主场 |
|
|
(2)求ξ的分布列,并用统计学知识说明两个队的实力情况.
考点:离散型随机变量及其分布列
专题:分类讨论,概率与统计
分析:(1)根据题意:甲胜2场,负1场,即甲队对主场胜2场和甲队主场胜1场,根据已知概率求解即可.
(2)根据题意可得:ξ=3,4,5,6,分别求解:P(ξ=3)=
,P(ξ=4)=
×
×
×
+
(
)2×
=
,P(ξ=5)=
,P(ξ=6)=
×(
)2×
=
,列出分布列,根据公式求解数学期望.
(2)根据题意可得:ξ=3,4,5,6,分别求解:P(ξ=3)=
| 2 |
| 27 |
| C | 1 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 2 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 9 |
| C | 2 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 27 |
解答:
解:(1)根据题意可得:
∵甲队得5分的情况是,甲胜2场,负1场,
∴甲队对主场胜2场和甲队主场胜1场,两种情况.
∴甲队得5分的概率为:
(
)2×
+
×
×
×
=
(2)甲、乙两队最后所得的总分分别为ξ、η,且ξ+η=9.
根据题意可得:ξ=3,4,5,6
∴P(ξ=3)=
,P(ξ=4)=
×
×
×
+
(
)2×
=
,
P(ξ=5)=
,P(ξ=6)=
×(
)2×
=
,
Eξ=3×
+4×
+5×
+6×
=
,∵Eξ+Eη=3×3=9,
∴Eη=
,说明两个队的实力相当,甲稍微强一点.
∵甲队得5分的情况是,甲胜2场,负1场,
∴甲队对主场胜2场和甲队主场胜1场,两种情况.
∴甲队得5分的概率为:
| C | 2 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| C | 1 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 9 |
(2)甲、乙两队最后所得的总分分别为ξ、η,且ξ+η=9.
根据题意可得:ξ=3,4,5,6
∴P(ξ=3)=
| 2 |
| 27 |
| C | 1 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 2 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
P(ξ=5)=
| 4 |
| 9 |
| C | 2 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 27 |
| ξ | 3 | 4 | 5 | 6 | ||||||||
| P |
|
|
|
|
| 2 |
| 27 |
| 1 |
| 3 |
| 4 |
| 9 |
| 4 |
| 27 |
| 14 |
| 3 |
∴Eη=
| 13 |
| 3 |
点评:本题考查了离散型的随机变量的概率与分布列,关键是确定随机变量的值,求解概率,属于中档题.

练习册系列答案
相关题目
过点P(-4,1)且与直线3x-4y+6=0垂直的直线方程是( )
| A、4x-3y-19=0 |
| B、4x+3y+13=0 |
| C、3x-4y-16=0 |
| D、3x+4y-8=0 |
已知复数z=
,则( )
| 2 |
| -1+i |
| A、z的实部为1 |
| B、z的虚部为-i |
| C、z的虚部为-1 |
| D、z的共轭复数为1+i |
在△ABC中,|
|=2,|
|=1,已知D是BC边上一点,AD平分∠BAC,
=λ
+μ
则( )
| AB |
| AC |
| AD |
| AB |
| AC |
A、λ=
| ||||
B、λ=
| ||||
C、λ=
| ||||
D、λ=
|
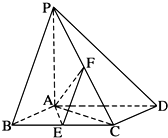 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.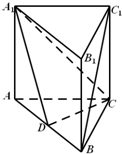 如图,在直三棱柱ABC-A1B1C1中,AC=BC=AA1,∠ACB=90°,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=AA1,∠ACB=90°,点D是AB的中点.