题目内容
3.已知函数f(x)=|lnx|,$g(x)=\left\{\begin{array}{l}0\\|{{x^2}-4}|-2\end{array}\right.$$\begin{array}{l}({0<x≤1})\\({x>1})\end{array}$则方程|f(x)+g(x)|=1实根的个数为( )| A. | 2个 | B. | 4个 | C. | 6个 | D. | 8个 |
分析 对x分类讨论:当0<x≤1时,显然可知有一实根$\frac{1}{e}$;当x>1时,方程可化为|x2-4|=1-lnx或|x2-4|=3-lnx,构造函数,画出函数图象,把方程问题转换为函数交点问题,利用数形结合思想判断即可得到答案.
解答 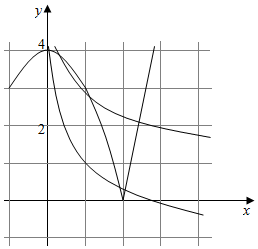 解:当0<x≤1时,
解:当0<x≤1时,
f(x)=-lnx,g(x)=0,
∴|f(x)+g(x)|=|-lnx|=1有一实根$\frac{1}{e}$;
当x>1时,
f(x)=lnx,g(x)=|x2-4|-2,
∴|f(x)+g(x)|=|lnx+g(x)|=1,
∴|x2-4|=1-lnx或|x2-4|=3-lnx,
分别画出函数的图象如图:
由图可知共有3个交点,
故实根的个数为4个,
故选:B.
点评 本题考查根的存在性与根的个数判断,考查数学转化思想方法,利用数形结合思想解决问题是关键,是中档题.

练习册系列答案
相关题目
13.已知函数f(x)=$\left\{\begin{array}{l}{ln(-x)+3,-2<x≤-1}\\{-{x}^{2}-2x+1,x>-1}\end{array}\right.$且f(2a)-$\frac{1}{2}$(2a+2)2<f(12-a)-$\frac{1}{2}$(14-a)2,则实数a的取值范围为( )
| A. | (2,4) | B. | (4,14) | C. | (2,14) | D. | (4,+∞) |
11.某城市关系要好的A,B,C,D四个家庭各有两个小孩共8人,分乘甲、乙两辆汽车出去游玩,每车限坐4名(乘同一辆车的4名小孩不考虑位置),其中A户家庭的孪生姐妹需乘同一辆车,则乘坐甲车的4名小孩恰有2名来自于同一个家庭的乘坐方式共有( )
| A. | 18种 | B. | 24种 | C. | 36种 | D. | 48种 |
18.若y=f(x)是定义域在R上的函数,则y=f(x)为奇函数的一个充要条件为( )
| A. | f(0)=0 | B. | 对?x∈R,f(x)=0都成立 | ||
| C. | ?x0∈R,使得f(x0)+f(-x0)=0 | D. | 对?x∈R,f(x)+f(-x)=0都成立 |
8.命题:“对于任意角θ,cos4θ-sin4θ=cos2θ”的证明过程:“cos4θ-sin4θ=(cos2θ-sin2θ)(cos2θ+sin2θ)=cos2θ-sin2θ=cos2θ”应用了( )
| A. | 分析法 | B. | 综合法 | ||
| C. | 综合法与分析法结合使用 | D. | 演绎法 |
3.设x、y满足不等式组$\left\{\begin{array}{l}{x-2y+1≤0}\\{2x+y-6≤0}\\{x-y+a≥0}\end{array}\right.$,其中a为常数,当且仅当x=y=1时,目标函数z=x+2y取得最小值,则目标函数z的最大值为( )
| A. | 8 | B. | $\frac{27}{5}$ | C. | 6 | D. | 3 |
20.若函数f(x)与函数g(x)的奇偶性相同,则称g(x)为f(x)的同心函数.那么,在下列给出的函数中,为函数f(x)=$\frac{{{x^2}-1}}{x}$的同心函数的是( )
| A. | g(x)=x+1 | B. | g(x)=2x | C. | g(x)=x2 | D. | g(x)=lnx |
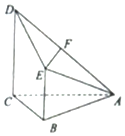 已知四棱锥A-BCDE中,侧面△ABC为等边三角形,BE=AB,CD=2AB,CD∥BE,且CD⊥平面ABC,F为棱AD的中点.
已知四棱锥A-BCDE中,侧面△ABC为等边三角形,BE=AB,CD=2AB,CD∥BE,且CD⊥平面ABC,F为棱AD的中点.