题目内容
4.已知函数$f(x)=\left\{\begin{array}{l}3-x,x<2\\{2^x}-3,x≥2\end{array}\right.$,若f(f(α))=1,则实数a的值为1,或log25.分析 由已知中函数$f(x)=\left\{\begin{array}{l}3-x,x<2\\{2^x}-3,x≥2\end{array}\right.$,结合f(f(α))=1,分类讨论,可得答案.
解答 解:∵函数$f(x)=\left\{\begin{array}{l}3-x,x<2\\{2^x}-3,x≥2\end{array}\right.$,
若f(f(α))=1,则f(α)=2,
则α=1,或α=log25,
故答案为:1,或log25
点评 本题考查的知识点是分段函数的应用,方程思想,分类讨论思想,难度中档.

练习册系列答案
相关题目
14.执行如图所示的程序框图,则输出的s的值是( )


| A. | 7 | B. | 6 | C. | 5 | D. | 3 |
12.已知集合A={x|1<x<3},B={x|x>2},则A∪∁RB=( )
| A. | {x|x≤2} | B. | {x|2<x<3} | C. | {x|x<3} | D. | {x|1<x≤2} |
19.已知实数a,b,c满足 ${(\frac{1}{3})^x}=2,{log_3}b=\frac{1}{2},{c^{-3}}=2$,则实数a,b,c的大小关系为( )
| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | b<a<c |
16.已知命题p:|x-a|<4,命题q:(x-2)(3-x)>0.若¬p是¬q的充分不必要条件,则实数a的取值范围是( )
| A. | [-1,6] | B. | (-∞,-1) | C. | (6,+∞) | D. | (-∞,-1)∪(6,+∞) |
13.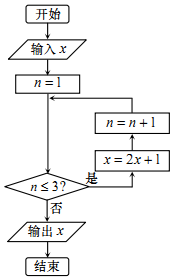 已知实数 x∈[1,10],执行如图所示的程序框图,则输出的x不大于63的概率为( )
已知实数 x∈[1,10],执行如图所示的程序框图,则输出的x不大于63的概率为( )
 已知实数 x∈[1,10],执行如图所示的程序框图,则输出的x不大于63的概率为( )
已知实数 x∈[1,10],执行如图所示的程序框图,则输出的x不大于63的概率为( )| A. | $\frac{3}{10}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{3}$ |
 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,且△ABC为等边三角形,AA1=AB=6,D为AC的中点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,且△ABC为等边三角形,AA1=AB=6,D为AC的中点.