题目内容
已知向量
=（sinA，cosA），
=（-
，-1），
∥
，且A为锐角，求∠A的大小．
| m |
| n |
| 3 |
| m |
| n |
考点：平面向量共线（平行）的坐标表示
专题：平面向量及应用
分析：由条件利用两个向量共线的性质求得tan A=
，结合A为锐角可得A的值．
| 3 |
解答：
解：∵向量
=（sinA，cosA），
=（-
，-1），
∥
，∴-sinA+
cosA=0，
求得 tan A=
，结合A为锐角可得A=
．
| m |
| n |
| 3 |
| m |
| n |
| 3 |
求得 tan A=
| 3 |
| π |
| 3 |
点评：本题主要考查两个向量共线的性质，根据三角函数的值求角，属于基础题．
练习册系列答案
相关题目
已知集合M={x|（x-1）2＞1，x∈R}，N={-1，0，1，2，3}，则M∩N=（ ）
| A、{-1，3} |
| B、{-1，0，3} |
| C、{0，2，3} |
| D、{1，2，3} |
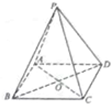如图，三棱锥P-ABCD的底面ABCD是正方形，顶点P在底面的射影是AC与BD的交点O，AB=2，∠PAC=60°．