题目内容
已知f(x)=
,数列{an}为首项是1,以f(1)为公比的等比数列;数列{bn}中b1=
,且bn+1=f(bn).
(1)求数列{an}和{bn}的通项公式;
(2)令cn=an(
-1),{cn}的前n项和为Tn,证明:对?n∈N+有Tn<4.
| x |
| 1+x |
| 1 |
| 2 |
(1)求数列{an}和{bn}的通项公式;
(2)令cn=an(
| 1 |
| bn |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)利用等差数列与等比数列的通项公式即可得出;
(2)利用等比数列的前n项和公式、“错位相减法”可得Tn=4-
.当n=1,2,3时,Tn<4;当n≥4时,利用二项式定理可得:2n-1=(1+1)n-1=(n-1)+(n-1)+…>2n-2≥n+2,可得
≤1,即可证明Tn<4.
(2)利用等比数列的前n项和公式、“错位相减法”可得Tn=4-
| 2+n |
| 2n-1 |
| n+2 |
| 2n-1 |
解答:
解:(1)f(1)=
,∵数列{an}为首项是1,以f(1)为公比的等比数列,∴an=(
)n-1.
∵bn+1=f(bn)=
,∴
=
+1,即
-
=1.
∴数列{
}是以
=2为首项,1为公差的等差数列,
∴
=2+(n-1)×1=n+1,
∴bn=
.
(2)cn=an(
-1)=
,
∴Tn=1+
+
+…+
+
,
Tn=
+
+…+
+
,
两式错位相减可得:
Tn=1+
+
+
-
=
-
=2-
.
∴Tn=4-
.
当n=1时,T1=1<4;
当n=2时,T2=2<4;
当n=3时,T3=
<4.
当n≥4时,
2n-1=(1+1)n-1=(n-1)+(n-1)+…>2n-2≥n+2,
∴
≤1,∴4-
≤3<4.
∴对?n∈N+有Tn<4.
| 1 |
| 2 |
| 1 |
| 2 |
∵bn+1=f(bn)=
| bn |
| 1+bn |
| 1 |
| bn+1 |
| 1 |
| bn |
| 1 |
| bn+1 |
| 1 |
| bn |
∴数列{
| 1 |
| bn |
| 1 |
| b1 |
∴
| 1 |
| bn |
∴bn=
| 1 |
| n+1 |
(2)cn=an(
| 1 |
| bn |
| n |
| 2n-1 |
∴Tn=1+
| 2 |
| 2 |
| 3 |
| 22 |
| n-1 |
| 2n-2 |
| n |
| 2n-1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 22 |
| n-1 |
| 2n-1 |
| n |
| 2n |
两式错位相减可得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| n |
| 2n |
1-
| ||
1-
|
| n |
| 2n |
| 2+n |
| 2n |
∴Tn=4-
| 2+n |
| 2n-1 |
当n=1时,T1=1<4;
当n=2时,T2=2<4;
当n=3时,T3=
| 11 |
| 4 |
当n≥4时,
2n-1=(1+1)n-1=(n-1)+(n-1)+…>2n-2≥n+2,
∴
| n+2 |
| 2n-1 |
| n+2 |
| 2n-1 |
∴对?n∈N+有Tn<4.
点评:本题考查了等差数列与等比数列的通项公式及其前n项和公式、“错位相减法”、二项式定理,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
函数f(x)=
x3-x2+a,函数g(x)=x2-3x,它们的定义域均为[1,+∞),并且函数f(x)的图象始终在函数g(x)的上方,那么a的取值范围是( )
| 1 |
| 3 |
| A、(0,+∞) | ||
| B、(-∞,0) | ||
C、(-
| ||
D、(-∞,
|
 幂函数y=xα中当α取不同的正数时,在[0,1]上它们的图象是一组美丽的曲线,设点A(1,0),B(0,1),若线段AB恰被两个幂函数y=xα,y=xβ的图象三等份,即BM=MN=NA,则αβ=( )
幂函数y=xα中当α取不同的正数时,在[0,1]上它们的图象是一组美丽的曲线,设点A(1,0),B(0,1),若线段AB恰被两个幂函数y=xα,y=xβ的图象三等份,即BM=MN=NA,则αβ=( ) 如图,三棱锥S-ABC,SA=SB=SC,SG为△SAB上的高,D、E、F为AC、BC、SC的中点.
如图,三棱锥S-ABC,SA=SB=SC,SG为△SAB上的高,D、E、F为AC、BC、SC的中点. 如图,已知扇形AOB的面积为
如图,已知扇形AOB的面积为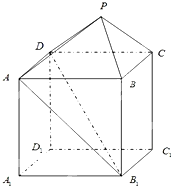 如图所示的几何体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,其中AB=2,BC=3,AA1=2,点P∈平面CC1D1D且PD=PC=
如图所示的几何体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,其中AB=2,BC=3,AA1=2,点P∈平面CC1D1D且PD=PC=