题目内容
11.若a1=3,an=an-1+$\frac{2}{{a}_{n-1}}$(n≥2),bn=$\frac{1}{{a}_{n}}$,写出bn的前3项.分析 a1=3,an=an-1+$\frac{2}{{a}_{n-1}}$(n≥2),分别取n=2,3,即可得出.
解答 解:∵a1=3,an=an-1+$\frac{2}{{a}_{n-1}}$(n≥2),
∴a2=${a}_{1}+\frac{2}{{a}_{1}}$=3+$\frac{2}{3}$=$\frac{11}{3}$,
a3=${a}_{2}+\frac{2}{{a}_{2}}$=$\frac{11}{3}$+$\frac{6}{11}$=$\frac{139}{33}$.
∵bn=$\frac{1}{{a}_{n}}$,
∴b1=$\frac{1}{3}$,b2=$\frac{3}{11}$,b3=$\frac{33}{139}$.
点评 本题考查了数列递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
19.为得到y=cos(2x-$\frac{π}{6}$)的图象,只需要将y=sin2x的图象( )
| A. | 向右平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向左平移$\frac{π}{6}$个单位 |
6.已知x=$\frac{π}{6}$是函数f(x)=asin x+bcosx的对称轴,则函数g(x)=bsinx-acosx的一条对称轴是( )
| A. | x=$\frac{π}{3}$ | B. | x=$\frac{2π}{3}$ | C. | x=$\frac{5π}{4}$ | D. | x=$\frac{π}{2}$ |
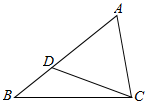 如图,在△ABC中,cosB=$\frac{11}{14}$,BC=7,点D在边AB上,且BD=3.
如图,在△ABC中,cosB=$\frac{11}{14}$,BC=7,点D在边AB上,且BD=3.