题目内容
3.已知P={x|x2-2x-15≤0},S={x|2-m≤x≤3+m},(1)是否存在实数m,使x∈P是x∈S的充要条件,若存在,求出m的取值范围.
(2)是否存在实数m,使x∈P是x∈S的必要条件,若存在,求出m的取值范围.
分析 (1)根据充要条件的定义建立方程关系进行求解即可.
(2)根据必要条件的定义建立不等式关系进行求解即可.
解答 解:P={x|x2-2x-15≤0}={x|-3≤x≤5},
(1)若存在实数m,使x∈P是x∈S的充要条件,
则满足$\left\{\begin{array}{l}{2-m≤3+m}\\{2-m=-3}\\{3+m=5}\end{array}\right.$,得$\left\{\begin{array}{l}{m≥-\frac{1}{2}}\\{m=5}\\{m=2}\end{array}\right.$,此时m无解,
即不存在实数m,使x∈P是x∈S的充要条件.
(2)若存在实数m,使x∈P是x∈S的必要条件,
则S⊆P,若2-m>3+m得m<-$\frac{1}{2}$,此时S=∅,满足条件.
若S≠∅,则满足$\left\{\begin{array}{l}{2-m≤3+m}\\{3+m≤5}\\{2-m≥-3}\end{array}\right.$,即$\left\{\begin{array}{l}{m≥-\frac{1}{2}}\\{m≤2}\\{m≤5}\end{array}\right.$,
即-$\frac{1}{2}$≤m≤2,
综上m≤2,
即存在m≤2使x∈P是x∈S的必要条件.
点评 本题主要考查充分条件和必要条件的应用,根据充分条件和必要条件的定义建立不等式关系是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
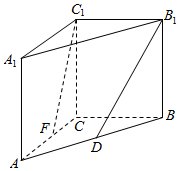 如图所示,在直三棱柱ABC-A1B1C1中,AC=4,BC=4,AA1=4,点D是AB的中点,点E是AC的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AC=4,BC=4,AA1=4,点D是AB的中点,点E是AC的中点.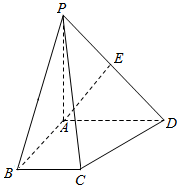 四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠BAD=90°,BC∥AD,PA=AB=BC=1,AD=2.
四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠BAD=90°,BC∥AD,PA=AB=BC=1,AD=2.