题目内容
6.已知x=$\frac{π}{6}$是函数f(x)=asin x+bcosx的对称轴,则函数g(x)=bsinx-acosx的一条对称轴是( )| A. | x=$\frac{π}{3}$ | B. | x=$\frac{2π}{3}$ | C. | x=$\frac{5π}{4}$ | D. | x=$\frac{π}{2}$ |
分析 由条件利用f(0)=f($\frac{π}{3}$),求得b=$\sqrt{3}$a,再根据两角和的正弦公式化简g(x)的解析式,利用正弦函数的图象的对称性,得出结论.
解答 解:∵函数f(x)=asin x+bcosx,∵x=$\frac{π}{6}$是f(x)的图象的对称轴,
∴f(0)=f($\frac{π}{3}$),即 b=$\frac{\sqrt{3}•a+b}{2}$,求得b=$\sqrt{3}$a,
则函数g(x)=bsinx-acosx=$\sqrt{3}$asinx-acosx=2asin(x-$\frac{π}{6}$),
令x-$\frac{π}{6}$=kπ+$\frac{π}{2}$,k∈Z,可得x=kπ+$\frac{2π}{3}$,k∈Z,故g(x)的图象的对一条对称轴是x=$\frac{2π}{3}$,
故选:B.
点评 本题主要考查正弦函数、余弦函数的图象的对称性,属于基础题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
16.命题“?x∈R,f(x)g(x)≠0”的否定是( )
| A. | ?x∈R,f(x)=0且g(x)=0 | B. | ?x∈R,f(x)=0或g(x)=0 | ||
| C. | ?x0∈R,f(x0)=0且g(x0)=0 | D. | ?x0∈R,f(x0)=0或g(x0)=0 |
17.某几何体的三视图及其尺寸如图所示,则该几何体的各侧面中,最大的侧面的面积为( )
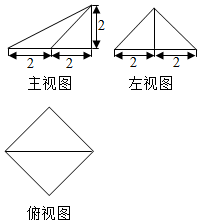

| A. | 4 | B. | 8 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{6}$ |
16.已知函数f(x)=$\left\{\begin{array}{l}{{log}_{2}x,x≥1}\\{x^2+m^2,x<1}\end{array}\right.$,若f(f(-1))=2,在实数m的值为( )
| A. | 1 | B. | 1或-1 | C. | $\sqrt{3}$ | D. | $\sqrt{3}$或-$\sqrt{3}$ |
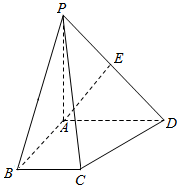 四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠BAD=90°,BC∥AD,PA=AB=BC=1,AD=2.
四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠BAD=90°,BC∥AD,PA=AB=BC=1,AD=2.