题目内容
20.已知正数x,y满足x2+2xy-3=0,则2x+y的最小值是3.分析 用x表示y,得到2x+y关于x的函数,利用基本不等式得出最小值.
解答 解:∵x2+2xy-3=0,∴y=$\frac{3-{x}^{2}}{2x}$,
∴2x+y=2x+$\frac{3-{x}^{2}}{2x}$=$\frac{3{x}^{2}+3}{2x}$=$\frac{3x}{2}+\frac{3}{2x}$≥2$\sqrt{\frac{3x}{2}•\frac{3}{2x}}$=3.
当且仅当$\frac{3x}{2}=\frac{3}{2x}$即x=1时取等号.
故答案为:3.
点评 本题考查了基本不等式的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.4名同学参加3项不同的课外活动,若每名同学可自由选择参加其中的一项,则每项活动至少有一名同学参加的概率为( )
| A. | $\frac{4}{9}$ | B. | $\frac{4}{27}$ | C. | $\frac{9}{64}$ | D. | $\frac{3}{64}$ |

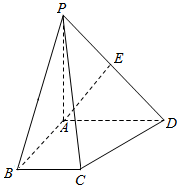 四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠BAD=90°,BC∥AD,PA=AB=BC=1,AD=2.
四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠BAD=90°,BC∥AD,PA=AB=BC=1,AD=2.