题目内容

函数f（x）=
sinx
2-cosx
，则f′（0）的值为
 
．
考点：导数的运算
专题：导数的概念及应用
分析：先根据导数的运算法则求导，再代入值计算即可．
解答： 解：∵f（x）=
sinx
2-cosx
，
∴f′（x）=
(sinx)′(2-cosx)-sinx(2-cosx)′
(2-cosx)2
=
cosx(2-cosx)-sinxsinx
(2-cosx)2
=
2cosx-1
(2-cosx)2
，
∴f′（0）=
1
1
=1，
故答案为：1．
点评：本题考查了导数的运算法则和函数值得求法，属于基础题
练习册系列答案
相关题目
已知函数f（x）=
-
1
2
x+
1
4
，x∈[0，
1
2
]
2x2
x+2
，x∈(
1
2
，1]
，g（x）=asin（
π
3
x+
3π
2
）-2a+2（a＞0），给出下列结论，其中所有正确的结论的序号是（　　）
①直线x=3是函数g（x）的一条对称轴；         
②函数f（x）的值域为[0，
2
3
]；
③若存在x1，x2∈[0，1]，使得f（x1）=g（x2），则实数a的取值范围是[
4
9
，
4
5
]；
④对任意a＞0，方程f（x）=g（x）在[0，1]内恒有解．
A、①②B、①②③
C、①③④D、①②④
函数f（x）=log2|2x-1|的图象大致是（　　）
A、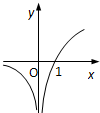
B、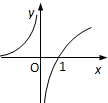
C、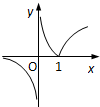
D、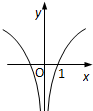
关于函数f（x）=sin2x-（
2
3
）|x|+
1
2
有如下四个结论：①f（x）的图象关于y轴对称；②f（x）的值域是（-
1
2
，
3
2
）；③当x∈（0，
π
2
）时，f（x）为增函数；④f（x）在R上有且只有一个零点，则正确结论的个数是（　　）
A、1B、2C、3D、4
求函数y=2x-3+
x2-12
的值域．
已知函数f（x）=
ln(x-a)
x
．
（Ⅰ）若a=-1，证明：函数f（x）是（0，+∞）上的减函数；
（Ⅱ）若曲线y=f（x）在点（1，f（1））处的切线与直线x-y=0平行，求a的值；
（Ⅲ）若x＞0，证明：
ln(x+1)
x
＞
x
ex-1
（其中e=2.71828…是自然对数的底数）．
设a=（
3
2
，1+sinα），b=（1-
2
2
，
1
3
），且a∥b，则锐角α为（　　）
A、30°B、45°
C、60°D、75°
设M={平面内的点（a，b）}，N={f（x）|f（x）=acos2x+bsin2x}，给出M到N的映射f：（a，b）→f（x）=acos2x+bsin2x，则点（1，
3
）的象f（x）的最小正周期为（　　）
A、
π
2
B、
π
4
C、π
D、2π
已知复数z=1-i（其中i为虚数单位），则
2i
z
等于（　　）
A、1-iB、1+i
C、-1-iD、-1+i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网