题目内容
3．在等差数列{an}中，前n项和为Sn，$\frac{S_2}{S_4}=\frac{1}{3}$，则$\frac{S_4}{S_8}$等于（ ）| A． | $\frac{3}{10}$ | B． | $\frac{1}{8}$ | C． | $\frac{1}{9}$ | D． | $\frac{1}{3}$ |
分析 根据等差数列的前n项和公式得到a1=$\frac{3}{2}$d，即可求出答案．
解答 解：设首项为a1，公差为d，
∵$\frac{S_2}{S_4}=\frac{1}{3}$，
∴$\frac{2{a}_{1}+d}{4{a}_{1}+6d}$=$\frac{1}{3}$，
即a1=$\frac{3}{2}$d，
则$\frac{S_4}{S_8}$=$\frac{4{a}_{1}+6d}{8{a}_{1}+28d}$=$\frac{6d+6d}{12d+28d}$=$\frac{3}{10}$，
故选：A．
点评 本题考查了等差数列的前n项和公式，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
13．已知函数f（x）=x2+（a+8）x+a2+a-12（a＜0），且f（a2-4）=f（2a-8），则$\frac{f（n）-4a}{n+1}（n∈{N^+}）$的最小值为（ ）
| A． | $\frac{37}{4}$ | B． | $\frac{35}{8}$ | C． | $\frac{28}{3}$ | D． | $\frac{27}{4}$ |
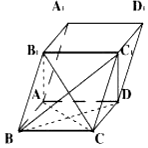如图，斜四棱柱ABCD-A1B1C1D1的底面是边长为$\sqrt{3}$的正方形，侧面A1ABB1⊥底面ABCD，AA1=2，∠B1BA=30°．