题目内容
已知数列{an}的通项公式an=
(n∈N),若bn=log
an2,且Sn是数列{bn}的前n项和,当n≥5时,试证明anSn<1.
| 1 |
| 2n |
| 1 |
| 2 |
考点:数列与不等式的综合
专题:等差数列与等比数列
分析:由已知条件推导出当n≥5时,试证明anSn<1等价于证明当n≥5时,
<1.用数学归纳法证明:①当n=5时,
=
<1,命题成立.②假设n=k时命题成立,即
<1,推导出当n=k+1时,
<1,命题也成立,由此能证明当n≥5时,anSn<1总成立.
| n(n+1) |
| 2n |
| 5×6 |
| 25 |
| 15 |
| 16 |
| k(k+1) |
| 2k |
| (k+1)(k+2) |
| 2k+1 |
解答:
证明:∵an=
(n∈N),∴bn=log
an2=2log
(
)=2n,
∴Sn=2(1+2+3+…+n)=n(n+1),
∵当n≥5时,试证明anSn<1等价于证明当n≥5时,
<1.
下面用数学归纳法证明:
①当n=5时,
=
<1,命题成立.
②假设n=k时命题成立,即
<1,
则当n=k+1时,
=
+
<
+
,
设cn=
,则cn+1-cn=
-
=
<0,
即{cn}为递减数列,
当n≥5时,cn≤c5=
<
,
∴
<1,命题也成立,
综上①②,得当n≥5时,anSn<1总成立.
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2n |
∴Sn=2(1+2+3+…+n)=n(n+1),
∵当n≥5时,试证明anSn<1等价于证明当n≥5时,
| n(n+1) |
| 2n |
下面用数学归纳法证明:
①当n=5时,
| 5×6 |
| 25 |
| 15 |
| 16 |
②假设n=k时命题成立,即
| k(k+1) |
| 2k |
则当n=k+1时,
| (k+1)(k+2) |
| 2k+1 |
| k(k+1) |
| 2k+1 |
| 2(k+1) |
| 2k+1 |
| 1 |
| 2 |
| k+1 |
| 2k |
设cn=
| n+1 |
| 2n |
| n+2 |
| 2n+1 |
| n+1 |
| 2n |
| -n |
| 2n |
即{cn}为递减数列,
当n≥5时,cn≤c5=
| 3 |
| 16 |
| 1 |
| 2 |
∴
| (k+1)(k+2) |
| 2k+1 |
综上①②,得当n≥5时,anSn<1总成立.
点评:本题考查不等式的证明,解题时要认真审题,注意数列的通项公式和前n项和公式的求法,注意数学归纳法的合理运用.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
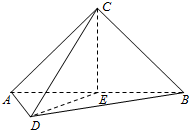 如图,在三棱锥C-ABD中,AC⊥CB,AC=CB,E为AB的中点,AD=DE=EC=2,CD=2
如图,在三棱锥C-ABD中,AC⊥CB,AC=CB,E为AB的中点,AD=DE=EC=2,CD=2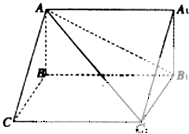 如图,在三棱柱ABC-A1B1C1中,已知AB=BC=1,CC1=2,AC1与平面BCC1B1所成角为30°,AB⊥平面BB1C1C.
如图,在三棱柱ABC-A1B1C1中,已知AB=BC=1,CC1=2,AC1与平面BCC1B1所成角为30°,AB⊥平面BB1C1C.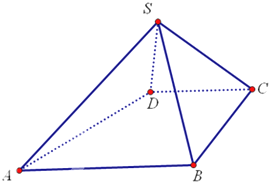 如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=SD=1.
如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=SD=1.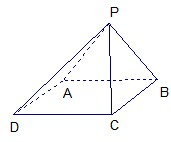 已知四棱锥P-ABCD的底面为菱形,且∠ABC=60°,AB=PC=2,AP=BP=
已知四棱锥P-ABCD的底面为菱形,且∠ABC=60°,AB=PC=2,AP=BP=