题目内容
设数列{an}的前n项和Sn=2n2,{bn}为等比数列,且a1=b1,b1(a2-a1)=b2.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)设Cn=
,求数列{cn}前n项和Tn.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)设Cn=
| anbn |
| 4 |
考点:数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)当n=1时,a1=S1=2;当n≥2时,an=Sn-Sn-1=2n2-2(n-1)2=4n-2,由此能求出{an}的通项公式;由{bn}为等比数列,且a1=b1,b1(a2-a1)=b2,能求出{bn}的通项公式.
(Ⅱ)由cn=
=
=(2n-1)4n-1,利用错位相减法能求出数列{cn}前n项和Tn.
(Ⅱ)由cn=
| anbn |
| 4 |
| (4n-2)4n-1 |
| 4 |
解答:
解:(Ⅰ)∵数列{an}的前n项和Sn=2n2,
∴当n=1时,a1=S1=2;
当n≥2时,an=Sn-Sn-1=2n2-2(n-1)2=4n-2,
n=1时,4n-2=2=a1,…(4分)
∴{an}的通项公式为an=4n-2.
∵{bn}为等比数列,且a1=b1,b1(a2-a1)=b2,
∴b1=2,b1×4=b2,∴bn=2•4n-1.…(6分)
(Ⅱ)∵cn=
=
=(2n-1)4n-1,
∴Tn=1+3×4+5×42+…+(2n-1)×4n-1,
4Tn=1×4+3×42+5×43+…+(2n-1)×4n,…(8分)
两式相减得:
3Tn=-1-2(4+42+…+4n-1)+(2n-1)•4n
=
[(6n-5)•4n+5],…(10分)
∴Tn=
[(6n-5)4n+5].…(12分)
∴当n=1时,a1=S1=2;
当n≥2时,an=Sn-Sn-1=2n2-2(n-1)2=4n-2,
n=1时,4n-2=2=a1,…(4分)
∴{an}的通项公式为an=4n-2.
∵{bn}为等比数列,且a1=b1,b1(a2-a1)=b2,
∴b1=2,b1×4=b2,∴bn=2•4n-1.…(6分)
(Ⅱ)∵cn=
| anbn |
| 4 |
| (4n-2)4n-1 |
| 4 |
∴Tn=1+3×4+5×42+…+(2n-1)×4n-1,
4Tn=1×4+3×42+5×43+…+(2n-1)×4n,…(8分)
两式相减得:
3Tn=-1-2(4+42+…+4n-1)+(2n-1)•4n
=
| 1 |
| 3 |
∴Tn=
| 1 |
| 9 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
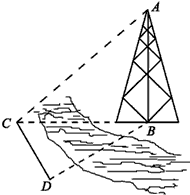 如图所示,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30m,并在点C处测得塔顶A的仰角为60°,求塔高AB.
如图所示,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30m,并在点C处测得塔顶A的仰角为60°,求塔高AB.