题目内容
17.已知点A(-2,-1),B(2,1),直线AM,BM相交于点M,且它们的斜率之积为-$\frac{1}{2}$,点M的轨迹为曲线H.(1)求曲线H的方程;
(2)过点P(-2,1)作斜率为k1,k2的两条直线l1,l2分别与曲线H交于C,D两点,且C,D关于原点对称,设点Q(-2,0)到直线l1,l2的距离分别为d1,d2且d1>d2,求k1的取值范围.
分析 (1)利用直接法求曲线H的方程;
(2)确定${{k}_{2}}^{2}$=$\frac{1}{4{{k}_{1}}^{2}}$,利用d1>d2,得$\frac{1}{\sqrt{{{k}_{1}}^{2}+1}}$>$\frac{1}{\sqrt{\frac{1}{4{{k}_{1}}^{2}}+1}}$,即可求k1的取值范围.
解答 解:(1)设M(x,y),则$\frac{y+1}{x+2}•\frac{y-1}{x-2}$=-$\frac{1}{2}$,
化简,可得曲线H的方程为$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{3}$=1;
(2)PC的方程为y-1=k1(x+2),PB的方程为y-1=k2(x+2),
∵k1k2=-$\frac{1}{2}$,∴${{k}_{2}}^{2}$=$\frac{1}{4{{k}_{1}}^{2}}$,
∵d1>d2,
∴$\frac{1}{\sqrt{{{k}_{1}}^{2}+1}}$>$\frac{1}{\sqrt{\frac{1}{4{{k}_{1}}^{2}}+1}}$,
∴$0<{k}_{1}<\frac{\sqrt{2}}{2}$.
点评 本题考查轨迹方程,考查斜率的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
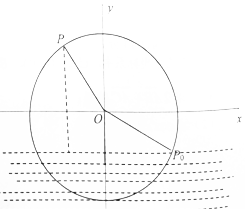 一半径为4米的水轮如图所示,水轮圆心O距离水面2米,已知水轮每60秒逆时针转动5圈,如果当水轮上点P从水中浮现时(图象P0点)开始计算时间,且点P距离水面的高度f(t)(米)与时间t(秒)满足函数:f(t)=Asin(ω+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).
一半径为4米的水轮如图所示,水轮圆心O距离水面2米,已知水轮每60秒逆时针转动5圈,如果当水轮上点P从水中浮现时(图象P0点)开始计算时间,且点P距离水面的高度f(t)(米)与时间t(秒)满足函数:f(t)=Asin(ω+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).