题目内容
7．设函数f（x）=ln x-$\frac{1}{2}$ax2-x，若x=1是f（x）的极值点，则a的值为（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 求出函数的导数，利用函数的极值点，列出方程求解即可．
解答 解：函数f（x）=ln x-$\frac{1}{2}$ax2-x，的定义域为：x＞0，
函数的导数为：y′=$\frac{1}{x}-ax-1$，
x=1是f（x）的极值点，
可得1-a-1=0，解得a=0．
经检验可知a=0时，x=1是f（x）的极值点，
故选：A．
点评 本题考查函数的极值的求法，导数的应用，考查计算能力．
练习册系列答案
相关题目
17．已知定义在实数集R上的函数f（x）满足下列三个条件
①对任意的x∈R，都有f（x+4）=f（x）．
②对于任意的x1，x2∈[0，2]，x1＜x2，都有f（x1）＜f（x2）．
③函数f（x+2）的图象关于y轴对称．则下列结论中，正确的是（ ）
①对任意的x∈R，都有f（x+4）=f（x）．
②对于任意的x1，x2∈[0，2]，x1＜x2，都有f（x1）＜f（x2）．
③函数f（x+2）的图象关于y轴对称．则下列结论中，正确的是（ ）
| A． | f（4.5）＜f（6.5）＜f（7） | B． | f（4.5）＜f（7）＜f（6.5） | C． | f（7）＜f（6.5）＜f（4.5） | D． | f（7）＜f（4.5）＜f（6.5） |
12．设角α的终边经过点P（sin2，cos2），则$\sqrt{2（1-sinα）}$的值等于（ ）
| A． | sin1 | B． | cos1 | C． | 2sin1 | D． | 2cos1 |
19．对于使不等式f（x）≤M成立的所有常数M中，我们把M的最小值叫做函数f（x）的上确界．若a，b∈R+，a+b=1，则$-\frac{1}{2a}-\frac{2}{b}$的上确界为（ ）
| A． | $-\frac{9}{2}$ | B． | $\frac{9}{2}$ | C． | $\frac{1}{4}$ | D． | -4 |
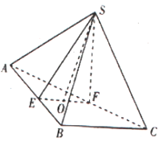如图，三棱锥S-ABC，E，F分别在线段AB，AC上，EF∥BC，△ABC，△SEF均是等边三角形，且平面SEF⊥平面ABC，若BC=4，EF=a，O为EF的中点．