题目内容
8.在△ABC中,a=15,b=10,A=60°,CE、CF三等分∠C,求CE、CF的长.分析 利用正弦定理可求sinB,结合大边对大角可得B为锐角,可得B=35.26°,进而可求C,设三等分角为x,则x=28.25°,在△BEC中,由正弦定理可求CE,在△ACF中,正弦定理可求FC的值.
解答 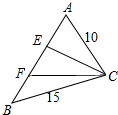 解:∵a=15,b=10,A=60°,
解:∵a=15,b=10,A=60°,
∴sinB=$\frac{bsinA}{a}$=$\frac{10×\frac{\sqrt{3}}{2}}{15}$=$\frac{\sqrt{3}}{3}$.
∴b<a,可得:B为锐角,B=35.26°,
∴C=180°-A-B=84.74°,
∴由CE、CF三等分∠C,设三等分角为x,则x=28.25°,
在△BEC中,正弦定理$\frac{CE}{sinB}=\frac{a}{sin(180°-B-2x)}$,可得:CE=$\frac{asinB}{sin(180°-B-2x)}$=$\frac{15×sin35.26°}{sin116.24°}$=9.65.
在△ACF中,正弦定理$\frac{FC}{sinA}=\frac{b}{sin(180°-A-2x)}$,可得:FC=$\frac{bsinA}{sin(180°-A-2x)}$=$\frac{10×sin60°}{sin91.75°}=8.66$
点评 本题主要考查了正弦定理在解三角形中的应用,考查了计算能力和转化思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.设定义在(0,+∞)上的单调函数f(x)对任意的x∈(0,+∞)都有f(f(x)-log2x)=6,则不等式f(a2+a)>5的解集为( )
| A. | {a|a>1} | B. | {a|a<-2或a>1} | C. | {a|-2<a<1} | D. | {a|a<-2} |
14.设函数f(x)=lnx+x-a(a∈R),若存在b∈[1,e](e使自然对数的底数),使f(f(b))=b成立,则a的取值范围是( )
| A. | [1,e+1] | B. | [1,e] | C. | [0,1] | D. | [0,e] |