题目内容
18.已知向量$\overrightarrow{a}$=(2cosα,2sinα),$\overrightarrow{b}$=(-sinα,cosα),$\overrightarrow{x}$=$\overrightarrow{a}$+(t2-3)$\overrightarrow{b}$,$\overrightarrow{y}$=-k$\overrightarrow{a}$+$\overrightarrow{b}$,且$\overrightarrow{x}$•$\overrightarrow{y}$=0.(1)求函数k=f(t)的表达式;
(2)若t∈[-1,3],求f(t)的最大值与最小值.
分析 (1)由向量的数量积运算和三角函数公式可得;
(2)由二次函数区间的最值可得.
解答 解:(1)∵向量$\overrightarrow{a}$=(2cosα,2sinα),$\overrightarrow{b}$=(-sinα,cosα),$\overrightarrow{x}$=$\overrightarrow{a}$+(t2-3)$\overrightarrow{b}$,$\overrightarrow{y}$=-k$\overrightarrow{a}$+$\overrightarrow{b}$,且$\overrightarrow{x}$•$\overrightarrow{y}$=0,
∴${\overrightarrow{a}}^{2}$=4cos2α+4sin2α=4,${\overrightarrow{b}}^{2}$=cos2α+sin2α=1,$\overrightarrow{a}•\overrightarrow{b}$=-2cosαsinα+2sinαcosα=0
∴$\overrightarrow{x}$•$\overrightarrow{y}$=-k${\overrightarrow{a}}^{2}$+(t2-3)${\overrightarrow{b}}^{2}$+(1+3k-kt2)$\overrightarrow{a}•\overrightarrow{b}$=-4k+(t2-3)=0,
∴k=f(t)=$\frac{1}{4}$(t2-3);
(2)由二次函数可知,f(t)=$\frac{1}{4}$(t2-3)图象为开口向上的抛物线,
对称轴为t=0,故当t=0时,函数取最小值-$\frac{3}{4}$,
当t=3时,函数取最大值$\frac{3}{2}$.
点评 本题考查三角函数的运算,涉及平面向量的数量积和二次函数区间的最值,属基础题.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案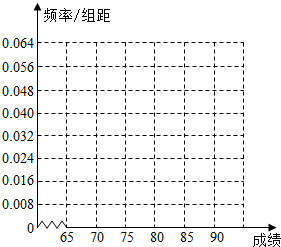 在党的群众教育路线总结阶段,一督导组从某单位随机抽调25名员工,让他们对本单位的各项开展工作进行打分评价,现获得如下的数据:70,82,81,76,84,80,77,77,65,85,69,83,71,76,89,74,73,83,78,82,72,74,86,79,76,根据上述数据得到样本的频率分布表如下:
在党的群众教育路线总结阶段,一督导组从某单位随机抽调25名员工,让他们对本单位的各项开展工作进行打分评价,现获得如下的数据:70,82,81,76,84,80,77,77,65,85,69,83,71,76,89,74,73,83,78,82,72,74,86,79,76,根据上述数据得到样本的频率分布表如下:(1)根据上述数据完成样本的频率分布表;
(2)根据(1)频率分布表,完成样本频率分布直方图;
(3)根据样本频率分布直方图,以频率作为概率,求在该单位中任取6名员工的打分,他们的打分在(75,85]内的人员数X的数学期望.
| 分组 | 频数 | 频率 |
| [65,70] | ||
| (70,75] | ||
| (75,80] | ||
| (80,85] | ||
| (85,90] |
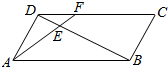 如图,点E是平行四边形ABCD对角线BD的n(n∈N且n≥2)等分点中最靠近点D的那点.线段AE的延长线交CD于点F,若向量$\overrightarrow{AF}=\frac{1}{n-1}\overrightarrow{AB}+x\overrightarrow{AD}$,则实数x的值为1.
如图,点E是平行四边形ABCD对角线BD的n(n∈N且n≥2)等分点中最靠近点D的那点.线段AE的延长线交CD于点F,若向量$\overrightarrow{AF}=\frac{1}{n-1}\overrightarrow{AB}+x\overrightarrow{AD}$,则实数x的值为1.