题目内容
方程lg（lnx）=0的解为x等于（ ）
| A、1 | B、e | C、10 | D、π |
考点：对数的运算性质
专题：函数的性质及应用
分析：利用对数的运算性质即可得出．
解答：
解：∵lg（lnx）=0，
∴lnx=1，
∴x=e．
故选：B．
∴lnx=1，
∴x=e．
故选：B．
点评：本题考查了对数的运算性质，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知全集U=R，A={x|x＞1}，B={x|x2-2x＞0}，则∁U（A∪B）=（ ）
| A、{x|x≤2} |
| B、{x|x≥1} |
| C、{x|0≤x≤1} |
| D、{x|0≤x≤2} |
下列函数中，与函数y=x相同的函数是（ ）
| A、y=|x| | ||
B、y=
| ||
C、y=(
| ||
| D、y=logaax（a＞0，且a≠1） |
已知向量
=（2k-3，-6），
=（2，1）且
∥
则实数k=（ ）
| a |
| c |
| a |
| c |
A、-
| ||
B、
| ||
| C、15 |
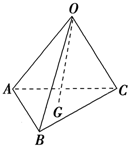如图，在三棱锥O-ABC中，G是△ABC的重心，若| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| c |
| OG |
A、
| ||||||
B、
| ||||||
| C、a+b+c | ||||||
| D、3a+3b+3c |