题目内容
13.已知圆M的方程为x2+(y-2)2=1,直线l的方程为x-2y=0,点P在直线l上,过P点作圆M的切线PA、PB,切点为A、B.(1)若点P的坐标为(0,0),求∠APB;
(2)若点P的坐标为(2,1),过P作直线与圆M交于C、D两点,当$CD=\sqrt{2}$时,求直线CD的方程;
(3)经过A、P、M三点的圆是否经过异于点M的定点,若经过,请求出此定点的坐标;若不经过,请说明理由.
分析 (1)求出MP=2,推出∠MPA=∠MPA=30°,即可求出∠APB.
(2)当直线斜率不存在时,不合题意;当直线斜率存在时,设直线CD方程为y-1=k(x-2),利用圆心M到直线CD的距离为$\frac{{\sqrt{2}}}{2}$,求出k没然后求解直线方程.
(3)设P(2m,m),MP的中点$Q(m,\frac{m}{2}+1)$,求出经过A、P、M三点的圆是以Q为圆心,MQ为半径的圆,
的方程,然后求解,交点坐标,推出经过A、P、M三点的圆经过异于点M的定点$({\frac{4}{5},\frac{2}{5}})$.
解答 解:(1)因为点P坐标为(0,0),所以MP=2,
又因为MA=MB=1,所以∠MPA=∠MPA=30°,故∠APB=60°.
(2)当直线斜率不存在时,不合题意;
当直线斜率存在时,设直线CD方程为y-1=k(x-2)
因为$CD=\sqrt{2}$,所以圆心M到直线CD的距离为$\frac{{\sqrt{2}}}{2}$,
由$\frac{{|{-2k-1}|}}{{\sqrt{1+{k^2}}}}=\frac{{\sqrt{2}}}{2}$,解得k=-1或$k=-\frac{1}{7}$,
故直线CD的方程为:x+y-3=0或x+7y-9=0.
(3)设P(2m,m),MP的中点$Q(m,\frac{m}{2}+1)$,
因为PA为圆M的切线,
所以经过A、P、M三点的圆是以Q为圆心,MQ为半径的圆,
故其方程为${(x-m)^2}+{(y-\frac{m}{2}-1)^2}={m^2}+{(\frac{m}{2}-1)^2}$
化简得x2+y2-2y-m(2x+y-2)=0,
由$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}-2y=0}\\{2x+y-2=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}x=\frac{4}{5}\\ y=\frac{2}{5}\end{array}\right.$,
所以经过A、P、M三点的圆经过异于点M的定点$({\frac{4}{5},\frac{2}{5}})$.
点评 本题考查圆的方程的综合应用,直线与圆的位置关系的应用,考查转化思想以及计算能力.

 小学课时特训系列答案
小学课时特训系列答案| A. | [-2,1) | B. | (1,2] | C. | [-2,-1) | D. | (-1,2] |
| 16 | 22 | 77 | 94 | 39 | 49 | 54 | 43 | 54 | 82 | 17 | 37 | 93 | 23 | 78 | 87 | 35 | 20 | 96 | 43 |
| 84 | 42 | 17 | 53 | 31 | 57 | 24 | 55 | 06 | 88 | 77 | 04 | 74 | 47 | 67 | 21 | 76 | 33 | 50 | 25 |
| A. | 23 | B. | 37 | C. | 35 | D. | 17 |
| A. | [0,$\frac{1}{8}$] | B. | [-1,0]∪(0,$\frac{1}{8}$] | C. | [-1,0] | D. | [-1,$\frac{1}{8}$] |
| A. | (0,$\frac{\sqrt{7}}{3}$] | B. | (0,$\frac{\sqrt{5}}{2}$] | C. | ($\sqrt{2}$,$\frac{5}{3}$] | D. | ($\sqrt{2}$,$\frac{\sqrt{13}}{3}$] |
| A. | $-\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
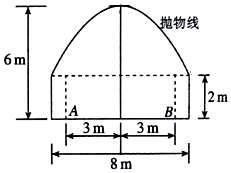 如图所示,一隧道内设双行线公路,其截面由一个长方形和抛物线构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米,已知行车道总宽度|AB|=6米,那么车辆通过隧道的限制高度是多少米?
如图所示,一隧道内设双行线公路,其截面由一个长方形和抛物线构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米,已知行车道总宽度|AB|=6米,那么车辆通过隧道的限制高度是多少米?