题目内容
16．若f（x）+${∫}_{0}^{1}$f（x）dx=x，则${∫}_{0}^{1}$f（x）dx=（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | 1 | D． | 2 |
分析 由f（x）=x-${∫}_{0}^{1}$f（x）dx，利用定积分的运算，求得${∫}_{0}^{1}$f（x）dx=$\frac{1}{2}$-${∫}_{0}^{1}$f（x）dx，即可求得答案．
解答 解：由f（x）+${∫}_{0}^{1}$f（x）dx=x，则f（x）=x-${∫}_{0}^{1}$f（x）dx，
则${∫}_{0}^{1}$f（x）dx=${∫}_{0}^{1}$（x-${∫}_{0}^{1}$f（x）dx）dx=${∫}_{0}^{1}$xdx-${∫}_{0}^{1}$[${∫}_{0}^{1}$f（x）dx]dx=$\frac{1}{2}$-${∫}_{0}^{1}$f（x）dx，
∴${∫}_{0}^{1}$f（x）dx=$\frac{1}{2}$-${∫}_{0}^{1}$f（x）dx，
则${∫}_{0}^{1}$f（x）dx=$\frac{1}{4}$，
故选A．
点评 本题考查定积分的运算，考查定积分的运算性质，属于基础题．
练习册系列答案
孟建平错题本系列答案
超能学典应用题题卡系列答案
相关题目
6．曲线y=xlnx在点（e，e）处的切线斜率为（ ）
| A． | e | B． | 2e | C． | 1 | D． | 2 |
11．已知双曲线Γ：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0）的一条渐近线为l，圆C：（x-a）2+y2=8与l交于A，B两点，若△ABC是等腰直角三角形，且$\overrightarrow{OB}=5\overrightarrow{OA}$（其中O为坐标原点），则双曲线Γ的离心率为（ ）
| A． | $\frac{{\sqrt{13}}}{3}$ | B． | $\frac{{2\sqrt{13}}}{3}$ | C． | $\frac{{\sqrt{13}}}{5}$ | D． | $\frac{{2\sqrt{13}}}{5}$ |
8．
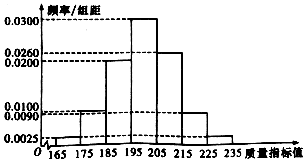某种产品的质量以其质量指标衡量，并依据质量指标值划分等级如表：
从某企业生产的这种产品中抽取200件，检测后得到如下的频率分布直方图：
（1）根据以上抽样调查的数据，能否认为该企业生产这种产品符合“一、二等品至少要占到全部产品的92%的规定”？
（2）在样本中，按产品等级用分层抽样的方法抽取8件，再从这8件产品中随机抽取4件，求抽取的4件产品中，一、二、三等品都有的概率；
（3）该企业为提高产品的质量，开展了“质量提升月”活动，活动后再抽样检测，产品质量指标值X近似满足X～N（218，140），则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少？
某种产品的质量以其质量指标衡量，并依据质量指标值划分等级如表：| 质量指标值m | m＜185 | 185≤m＜205 | M≥205 |
| 等级 | 三等品 | 二等品 | 一等品 |
（1）根据以上抽样调查的数据，能否认为该企业生产这种产品符合“一、二等品至少要占到全部产品的92%的规定”？
（2）在样本中，按产品等级用分层抽样的方法抽取8件，再从这8件产品中随机抽取4件，求抽取的4件产品中，一、二、三等品都有的概率；
（3）该企业为提高产品的质量，开展了“质量提升月”活动，活动后再抽样检测，产品质量指标值X近似满足X～N（218，140），则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少？
6．在△ABC中，a，b，c分别为角A，B，C所对的边，若（a+c+b）（b+a-c）=3ab，则C=（ ）
| A． | 150° | B． | 60° | C． | 120° | D． | 30° |