题目内容
在等腰梯形ABCD中，E，F分别是底边AB，CD的中点，把四边形AEFD沿直线EF折起后所在的平面记为α，P∈α，设PB，PC与α所成的角分别为θ1，θ2(θ1，θ2均不为零)．若θ1＝θ2，则点P的轨迹为( )
A．直线 B．圆
C．椭圆 D．抛物线
B
[解析] 如图，设B，C在平面α内的投影分别为M，N，连接PM，BM，CN，PN，MN，根据直线与平面所成角的意义，∠BPM＝θ1，∠CPN＝θ2，∵θ1＝θ2，
∴
＝
＝
，
又∵BE∥CF，∴＝＝
＝k≠1，
∴＝k，由于在平面内到两定点的距离之比等于不为1的常数的点的轨迹是圆，故选B.
练习册系列答案
阅读快车系列答案
相关题目
，若
时
，则
是
上的偶函数，且
在
上是增函数，若
，则
的取值范围是 
及底面边长
分别为多少时，这个水箱的表面积为最大？并求出这个水箱最大的表面积.（10）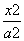
－
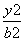＝1(a>0，b>0)与抛物线y2＝2px(p>0)的交点为A，B，A，B连线经过抛物线的焦点F，且线段AB的长等于双曲线的虚轴长，则双曲线的离心率为( )
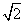B．2 C．3 D.
＝0(O为坐标原点)，且
|，则该双曲线的离心率为________．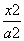
－
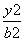＝1(a>0，b>0)的左、右焦点分别为F1，F2，点O为坐标原点，点P在双曲线右支上，△PF1F2内切圆的圆心为Q，圆Q与x轴相切于点A，过F2作直线PQ的垂线，垂足为B，则|OA|与|OB|的长度依次为( )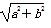
，
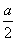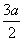D.
－
x2＋x＋1在区间
上有极值点，则实数a的取值范围是( )
为第二象限角，若
，则