题目内容
已知双曲线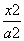
－
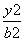＝1(a>0，b>0)的左、右焦点分别为F1，F2，点O为坐标原点，点P在双曲线右支上，△PF1F2内切圆的圆心为Q，圆Q与x轴相切于点A，过F2作直线PQ的垂线，垂足为B，则|OA|与|OB|的长度依次为( )
A．a，a B．a，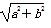
C.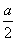
，
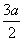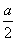D.，a
A
[解析] 设|AF1|＝x，|AF2|＝y，由双曲线定义得|PF1|－|PF2|＝2a，由三角形内切圆的性质得x－y＝2a，又∵x＋y＝2c，∴x＝a＋c，∴|OA|＝a.延长F2B交PF1于点C，∵PQ为∠F1PF2的角平分线，∴|PF2|＝|PC|，再由双曲线定义得|CF1|＝2a，∴|OB|＝a，故选A.
练习册系列答案
相关题目
的定义域为实数集R，求实数
的取值范围。
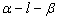，直线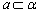
，
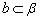，且a与l不垂直，b与l不垂直，那么( )
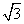，求p的值及圆F的方程；
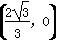，△ABC的三个顶点都在双曲线T上，O为坐标原点，设△ABC三条边AB，BC，AC的中点分别为M，N，P，且三条边所在直线的斜率分别为k1，k2，k3，ki≠0，i＝1,2,3.若直线OM，ON，OP的斜率之和为－1，则
＋
＋
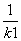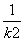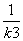的值为( )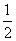
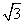，且其三个顶点均在抛物线E：x2＝2py(p>0)上．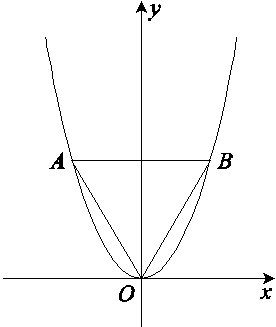
，其中f′(x)是f(x)的导函数，则不等式f(x3)<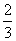
的解集为________．
，则
（ ）
B、
C、
D、