题目内容
已知二次函数f(x)=ax(x-1)(a≠0)且其图象的顶点恰好在函数y=log2x的图象上.
(1)求函数f(x)的解析式;
(2)若函数h(x)=|f(x)|+m恰有两个零点,求m的取值范围.
(1)求函数f(x)的解析式;
(2)若函数h(x)=|f(x)|+m恰有两个零点,求m的取值范围.
考点:二次函数的性质,函数解析式的求解及常用方法,函数零点的判定定理
专题:函数的性质及应用
分析:(1)先求出函数的顶点,根据顶点在函数y=log2x的图象上,顶点-
=
,解出a的值,从而求出函数的表达式;
(2)根据f(x)的解析式,由函数图象的对折变换得到函数y=|f(x)|的图象,再由h(x)=|f(x)|+m恰有2个零点,则函数y=|f(x)|的图象与直线y=-m有且只有两个交点,数形结合得到m的取值范围.
| a |
| 4 |
| log |
2 |
(2)根据f(x)的解析式,由函数图象的对折变换得到函数y=|f(x)|的图象,再由h(x)=|f(x)|+m恰有2个零点,则函数y=|f(x)|的图象与直线y=-m有且只有两个交点,数形结合得到m的取值范围.
解答:
解:(1)设f(x)=ax(x-1)(a≠0),
顶点坐标为(
,-
),
∵顶点在函数y=log2x的图象上,
∴-
=
,解得a=4,
∴f(x)=4x2-4x.
(2)由(1)得:f(x)=4x(x-1),
则函数y=|f(x)|的图象如下图所示:
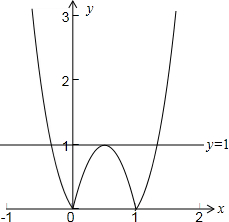
若h(x)=|f(x)|+m恰有2个零点,
则函数y=|f(x)|的图象与直线y=-m有且只有两个交点,
故-m>1,或-m=0,
则m<-1或m=0.
顶点坐标为(
| 1 |
| 2 |
| a |
| 4 |
∵顶点在函数y=log2x的图象上,
∴-
| a |
| 4 |
| log |
2 |
∴f(x)=4x2-4x.
(2)由(1)得:f(x)=4x(x-1),
则函数y=|f(x)|的图象如下图所示:

若h(x)=|f(x)|+m恰有2个零点,
则函数y=|f(x)|的图象与直线y=-m有且只有两个交点,
故-m>1,或-m=0,
则m<-1或m=0.
点评:本题考查的知识点是二次函数的图象和性质,对数函数的图象和性质,函数图象的对折变换,函数的零点,是函数的综合应用,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合P={x||x-1|<1},函数y=
的定义域为Q,则集合Q∩P=( )
| x-1 |
| A、{x|0<x≤1} |
| B、{x|0<x<2} |
| C、{x|1<x≤2} |
| D、{x|1<x<2} |
已知空间两个点A,B的坐标分别为A(1,2,2),B(2,-2,1),则|AB|=( )
| A、18 | ||
| B、12 | ||
C、3
| ||
D、2
|
 (理科选做)在四面体O-ABC中,点P为棱BC的中点.设
(理科选做)在四面体O-ABC中,点P为棱BC的中点.设