Question

9．已知A、B、C、D四点在半径为$\frac{5\sqrt{2}}{2}$的球面上，且AC=BD=5，AD=BC=$\sqrt{41}$，AB=CD，则三棱锥D-ABC的体积是20．

Answer 1

分析 构造长方体，其面上的对角线构成三棱锥D-ABC，计算出长方体的长宽高，即可求得三棱锥D-ABC的体积．

解答 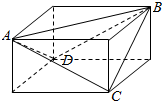解：由题意，构造长方体，其面上的对角线构成三棱锥D-ABC，如图所示，
设长方体的长宽高分别为a，b，c，
则$\left\{\begin{array}{l}{{a}^{2}+{b}^{2}+{c}^{2}=50}\\{{a}^{2}+{b}^{2}=25}\\{{a}^{2}+{c}^{2}=41}\end{array}\right.$，
解得a=4，b=3，c=5
∴三棱锥D-ABC的体积是V=4×3×5-4×$\frac{1}{3}×\frac{1}{2}×4×3×5$=20
故答案为：20．

点评 本题考查三棱锥体积的计算，考查学生的计算能力，构造长方体是关键．