题目内容
已知函数f(x)=a(x2+3)+bx+c,且关于x的不等式f(x)<2x+3a的解集为(-1,2).
(1)若关于x的方程f(x)=0有实数根,求实数a的取值范围;
(2)若函数f(x)不存在正实数零点,求实数a的取值范围.
(1)若关于x的方程f(x)=0有实数根,求实数a的取值范围;
(2)若函数f(x)不存在正实数零点,求实数a的取值范围.
考点:函数零点的判定定理,一元二次不等式的解法
专题:函数的性质及应用
分析:由关于x的不等式f(x)<2x+3a的解集为(-1,2).可得-1,2是关于x的方程f(x)=2x+3a,即ax2+(b-2)x+c=0的两根,结合韦达定理可得b=2-a,c=-2a,
(1)若关于x的方程f(x)=0有实数根,则△=b2-4a(c+3a)=-3a2-4a+4≥0,进而构造关于a的不等式,解得实数a的取值范围;
(2)若函数f(x)不存在正实数零点,则函数无零点,或只有非正零点,即△=b2-4a(c+3a)=-3a2-4a+4<0,或
,求实数a的取值范围.
(1)若关于x的方程f(x)=0有实数根,则△=b2-4a(c+3a)=-3a2-4a+4≥0,进而构造关于a的不等式,解得实数a的取值范围;
(2)若函数f(x)不存在正实数零点,则函数无零点,或只有非正零点,即△=b2-4a(c+3a)=-3a2-4a+4<0,或
|
解答:
解:∵关于x的不等式f(x)<2x+3a的解集为(-1,2).
∴-1,2是关于x的方程f(x)=2x+3a,即ax2+(b-2)x+c=0的两根,
∴-1+2=1=-
,-1×2=-2=
,(a≠0)
∴b=2-a,c=-2a,
(1)若关于x的方程f(x)=0有实数根,
则△=b2-4a(c+3a)=-3a2-4a+4≥0,
即3a2+4a-4≤0,
解得:a∈[-2,
],
∴a∈[-2,0)∪(0,
],
即实数a的取值范围为[-2,0)∪(0,
],
(2)若函数f(x)不存在正实数零点,
则△=b2-4a(c+3a)=-3a2-4a+4<0,此时a∈(-∞,-2)∪(
,+∞),
或
,即
解得:a∈(0,
]
综上所述,实数a的取值范围为(-∞,-2)∪(0,+∞),
∴-1,2是关于x的方程f(x)=2x+3a,即ax2+(b-2)x+c=0的两根,
∴-1+2=1=-
| b-2 |
| a |
| c |
| a |
∴b=2-a,c=-2a,
(1)若关于x的方程f(x)=0有实数根,
则△=b2-4a(c+3a)=-3a2-4a+4≥0,
即3a2+4a-4≤0,
解得:a∈[-2,
| 2 |
| 3 |
∴a∈[-2,0)∪(0,
| 2 |
| 3 |
即实数a的取值范围为[-2,0)∪(0,
| 2 |
| 3 |
(2)若函数f(x)不存在正实数零点,
则△=b2-4a(c+3a)=-3a2-4a+4<0,此时a∈(-∞,-2)∪(
| 2 |
| 3 |
或
|
|
解得:a∈(0,
| 2 |
| 3 |
综上所述,实数a的取值范围为(-∞,-2)∪(0,+∞),
点评:本题考查的知识点是函数零点的判定定理,一元二次不等式的解法,是方程,函数不等式的综合应用,难度中档.

练习册系列答案
相关题目
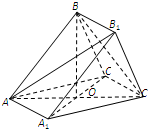 如图所示,三棱柱ABC-A1B1C1中,AB=AC=AA1=2,平面ABC1⊥平面A1ACC1,
如图所示,三棱柱ABC-A1B1C1中,AB=AC=AA1=2,平面ABC1⊥平面A1ACC1,