题目内容
9.某医院一天内派医生下乡医疗,派出医生数及概率如下:| 医生人数 | 0 | 1 | 2 | 3 | 4 | 5人以上 |
| 概率 | 0.1 | 0.16 | 0.2 | x | 0.2 | 0.04 |
(2)派出医生至多2人的概率.
(3)派出医生至少2 人的概率.
分析 (1)由某医院一天内派医生下乡医疗,派出医生数及概率统计表,能求出派出医生为3人的概率.
(2)派出医生至多2人是包含派出医生人数为0人,1人和2 人三种情况,利用互斥事件概率计算公式能求出派出医生至多2人的概率.
(3)派出医生至少2 人的对立事件包含派出医生人数为0人,1人两种情况,由此利用对立事件概率计算公式能求出派出医生人数至少2 人的概率.
解答 解:(1)由某医院一天内派医生下乡医疗,派出医生数及概率统计表,
得:派出医生为3人的概率p1=1-0.1-0.16-0.2-0.2-0.04=0.3.
(2)派出医生至多2人是包含派出医生人数为0人,1人和2 人三种情况,
∴派出医生至多2人的概率p2=0.1+0.16+0.2=0.46.
(3)派出医生至少2 人的对立事件包含派出医生人数为0人,1人两种情况,
∴派出医生人数至少2 人的概率p=1-0.1-0.16=0.74.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意互斥事件概率计算公式、对立事件概率计算公式的合理运用.

练习册系列答案
相关题目
20.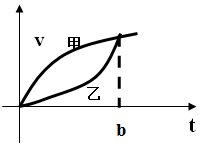 甲、乙速度v与时间t的关系如图,a(b)是t=b时的加速度,S(b)是从t=0到t=b的路程,则a甲(b)与a乙(b),S甲(b)与S乙(b)的大小关系是( )
甲、乙速度v与时间t的关系如图,a(b)是t=b时的加速度,S(b)是从t=0到t=b的路程,则a甲(b)与a乙(b),S甲(b)与S乙(b)的大小关系是( )
 甲、乙速度v与时间t的关系如图,a(b)是t=b时的加速度,S(b)是从t=0到t=b的路程,则a甲(b)与a乙(b),S甲(b)与S乙(b)的大小关系是( )
甲、乙速度v与时间t的关系如图,a(b)是t=b时的加速度,S(b)是从t=0到t=b的路程,则a甲(b)与a乙(b),S甲(b)与S乙(b)的大小关系是( )| A. | a甲(b)>a乙(b),S甲(b)>S乙(b) | B. | a甲(b)<a乙(b),S甲(b)<S乙(b) | ||
| C. | a甲(b)<a乙(b),S甲(b)>S乙(b) | D. | a甲(b)<a乙(b),S甲(b)<S乙(b) |
4.《九章算术》中的“两鼠穿墙题”是我国数学的古典名题:“今有垣厚若干尺,两鼠对穿,大鼠日一尺,小鼠也日一尺.大鼠日自倍,小鼠日自半.问何日相逢,各穿几何?题意是:有两只老鼠从墙的两边打洞穿墙.大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半”如果墙足够厚,Sn为前n天两只老鼠打洞长度之和,则S5=( )
| A. | $31\frac{15}{16}$ | B. | $32\frac{15}{16}$ | C. | $33\frac{15}{16}$ | D. | $26\frac{1}{2}$ |
18.若i是虚数单位,则计算$\frac{1+7i}{2-i}$的结果为( )
| A. | 1+3i | B. | 1-3i | C. | -1+3i | D. | -1-3i |
19.椭圆$\frac{{x}^{2}}{4}$+y2=1的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | 2 |
 函数f(x)是R上的奇函数,且当x>0时,函数的解析式为f(x)=log2(x+1).
函数f(x)是R上的奇函数,且当x>0时,函数的解析式为f(x)=log2(x+1).