题目内容
已知定义在R上的函数f (x)的周期为4,且当x∈(-1,3]时,f (x)=
,则函数g(x)=f(x)-1og6x的零点个数为( )
|
| A、4 | B、5 | C、6 | D、7 |
考点:分段函数的应用,函数零点的判定定理
专题:函数的性质及应用
分析:先根据函数的周期性画出函数y=f(x)的图象,以及y=log5x的图象,结合图象当x>6时,y=log6x>1此时与函数y=f(x)无交点,即可判定函数函数g(x)=f(x)-1og6x的零点个数.
解答:
解:根据周期性画出函数y=f(x)的图象,y=log6x的图象
当x=6时log66=1,
∴当x>6时y=log5x此时与函数y=f(x)无交点,
结合图象可知有5个交点,
则函数g(x)=f(x)-log6x的零点个数为5,
故选B.

当x=6时log66=1,
∴当x>6时y=log5x此时与函数y=f(x)无交点,
结合图象可知有5个交点,
则函数g(x)=f(x)-log6x的零点个数为5,
故选B.

点评:本题考查函数的零点,求解本题,关键是研究出函数f(x)性质,作出其图象,将函数g(x)=f(x)-1og6x的零点个数的问题转化为两个函数交点个数问题是本题中的一个亮点,此一转化使得本题的求解变得较容易.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知p:|2x-3|<1,q:x(x-3)<0,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知A={x|-2≤x≤7},B={x|-2≤x≤m+1},且A⊆B,则( )
| A、-2<m≤6 | B、m≥6 |
| C、m=6 | D、m=-3 |
函数y=x-ln(1+x)的单调递增区间为( )
| A、(-1,0) |
| B、(-∞,-1)和(0,+∞) |
| C、(0,+∞) |
| D、(-∞,-1) |
一个单位有职工800人,其中具有高级职称的职工120人,具有中级职称的职工360人,具有初级职称的职工200人,其余人员120人,为了解职工收入情况,决定采用分层抽样的方法,从中抽取容量为40的样本,则从上述各层中依次抽取的人数分别是( )
| A、12,24,15,9 |
| B、9,12,12,7 |
| C、8,15,12,5 |
| D、6,18,10,6 |
函数f(x)=lnx+2x-6的零点属于区间(n,n+1)(n∈z),则n等于( )
| A、1 | B、2 | C、3 | D、4 |
函数y=x3+ax2+bx的递减区间是(-1,2),则a,b的值为( )
A、a=-
| ||
B、a=-6,b=-
| ||
| C、a=3,b=2 | ||
| D、a=-3,b=-6 |
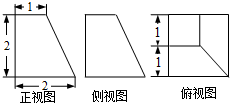 已知台体的体积公式V=
已知台体的体积公式V=