题目内容
函数y=x3+ax2+bx的递减区间是（-1，2），则a，b的值为（ ）
A、a=-
| ||
B、a=-6，b=-
| ||
| C、a=3，b=2 | ||
| D、a=-3，b=-6 |
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：先求出原函数的导数，导数f′（x）=3x2+2ax+b，∴函数y=x3+ax2+bx的递减区间应该在方程3x2+2ax+b=0的两根之间，所以-1，2是方程的两个根，所以带入方程便可求出a，b的值．
解答：
解：y′=3x2+2ax+b，则x=-1，或x=2是方程3x2+2ax+b=0两个根；
∴
，解得a=-
，b=-6．
故选：A．
∴
|
| 3 |
| 2 |
故选：A．
点评：本题的导函数是一个二次函数，小于0的解应该在两根之间，所以所给的单调递减区间和两根之间的区间应是同一个区间，所以x=-1，或x=2是方程的两个根．明白了这点，本题答案就不难求了．
练习册系列答案
相关题目
已知定义在R上的函数f （x）的周期为4，且当x∈（-1，3]时，f （x）=
，则函数g（x）=f（x）-1og6x的零点个数为（ ）
|
| A、4 | B、5 | C、6 | D、7 |
已知α+β=3π，下列等式恒成立的是（ ）
| A、sinα=sinβ |
| B、cosα=cosβ |
| C、sinα=cosβ |
| D、tanα=tanβ |
一只昆虫在边长分别为6，8，10的三角形区域内随机爬行，则其到三角形顶点的距离小于2的地方的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
命题P：“若m＞0，则方程x2+x-m=0有实数根”的否定是（ ）
| A、￢P：若m＞0，则方程x2+x-m=0没有实数根 |
| B、￢P：若方程x2+x-m=0没有实数根，则m≤0 |
| C、￢P：若m≤0，则方程x2+x-m=0没有实数根 |
| D、￢P：若m＜0，则方程x2+x-m=0没有实数根 |
设全集U={1，2，3，4}，集合S={l，3}，T={4}，则（∁US）∪T等于（ ）
| A、{2，4} | B、{4} |
| C、∅ | D、{1，3，4} |
函数y=xlnx的减区间为（ ）
A、（-∞，
| ||
B、（
| ||
C、（0，
| ||
| D、（0，+∞） |
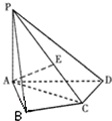如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，E是PC的中点．