题目内容
7.对于数列{an},定义数列{an+1-an}为数列{an}的“等差列”,若a1=2,{an}的“等差列”的通项公式为2n,则数列{an}的前2015项和S2015=( )| A. | 22016-1 | B. | 22016 | C. | 22016+1 | D. | 22016-2 |
分析 利用“累加求和”及其等比数列的前n项和公式可得an,再利用等比数列的前n项和公式即可得出.
解答 解:∵a1=2,{an}的“等差列”的通项公式为2n,
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=2n-1+2n-2+…+2+2
=$\frac{{2}^{n}-1}{2-1}$+1=2n.
∴数列{an}的前2015项和S2015=2+22+…+22015=$\frac{2({2}^{2015}-1)}{2-1}$=22016-2.
故选:D.
点评 本题考查了“累加求和”、等比数列的通项公式及其前n项和公式、递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.如图所示的程序框图的运行结果为( )


| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
12.已知函数f(x)=x2+x,若数列$\left\{{\frac{1}{f(n)}}\right\}$的前n项和为Sn,则S2014的值为( )
| A. | $\frac{2014}{2015}$ | B. | $\frac{2013}{2014}$ | C. | $\frac{2012}{2013}$ | D. | $\frac{2014}{2013}$ |
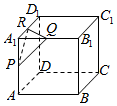 正方体ABCD-A1B1C1D1的棱长为1,点P,Q,R分别是棱A1A,A1B1,A1D1的中点,以△PQR为底面作正三棱柱.若此三棱柱另一底面的三个顶点也都在该正方体的表面上,则这个正三棱柱的高h=$\frac{\sqrt{3}}{2}$.
正方体ABCD-A1B1C1D1的棱长为1,点P,Q,R分别是棱A1A,A1B1,A1D1的中点,以△PQR为底面作正三棱柱.若此三棱柱另一底面的三个顶点也都在该正方体的表面上,则这个正三棱柱的高h=$\frac{\sqrt{3}}{2}$.