题目内容
2. 某校为了解全校高中学生五一小长假参加实践活动的情况,抽查了100名学生,统计他们假期参加实践活动的实践,绘成的频率分布直方图如图所示,这100名学生中参加实践活动时间在6-10小时内的人数为58.
某校为了解全校高中学生五一小长假参加实践活动的情况,抽查了100名学生,统计他们假期参加实践活动的实践,绘成的频率分布直方图如图所示,这100名学生中参加实践活动时间在6-10小时内的人数为58.
分析 利用频率分布直方图中,频率等于纵坐标乘以组距,求出在6-10小时外的频率;利用频率和为1,求出在6-10小时内的频率;利用频数等于频率乘以样本容量,求出这100名同学中学习时间在6-10小时内的同学的人数.
解答 解:由频率分布直方图知:(0.04+0.12+a+b+0.05)×2=1,
∴a+b=0.29,
∴参加实践活动时间在6-10小时内的频率为0.29×2=0.58,
∴这100名学生中参加实践活动时间在6-10小时内的人数为100×0.58=58.
故答案为:58
点评 本题考查的知识点是频率分布直方图,熟练掌握频率分布直方图中频率=矩形的高×组距,频数=频率×样本容量,是解答本题的关键.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
12.已知函数f(x)=x2+x,若数列$\left\{{\frac{1}{f(n)}}\right\}$的前n项和为Sn,则S2014的值为( )
| A. | $\frac{2014}{2015}$ | B. | $\frac{2013}{2014}$ | C. | $\frac{2012}{2013}$ | D. | $\frac{2014}{2013}$ |
10.老师提出一个关于引力波的问题需要甲、乙两位同学回答,已知甲、乙两位同学能回答该问题的概率为0.4和0.5.在这个问题已被解答的条件下,甲乙两位同学都能正确回答该问题的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{7}$ | C. | $\frac{2}{9}$ | D. | $\frac{9}{10}$ |
7.在极坐标系中,点A($\frac{\sqrt{2}}{2}$,$\frac{π}{6}$),B($\frac{\sqrt{2}}{2}$,$\frac{2π}{3}$),则线段AB中点的极坐标为( )
| A. | ($\frac{1}{2}$,$\frac{5π}{12}$) | B. | (1,$\frac{5π}{12}$) | C. | ($\frac{\sqrt{2}}{2}$,$\frac{5π}{12}$) | D. | ($\frac{\sqrt{2}}{2}$,$\frac{π}{3}$) |
14.已知数列an:$\frac{1}{1}$,$\frac{2}{1}$,$\frac{1}{2}$,$\frac{3}{1}$,$\frac{2}{2}$,$\frac{1}{3}$,$\frac{4}{1}$,$\frac{3}{2}$,$\frac{2}{3}$,$\frac{1}{4}$,…,依它的前10项的规律知a2106应为( )
| A. | $\frac{3}{61}$ | B. | $\frac{2}{61}$ | C. | $\frac{1}{63}$ | D. | $\frac{1}{64}$ |
12.设集合A={-1,0},集合B={0,1,2},则A∪B的子集个数是( )
| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
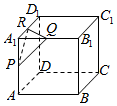 正方体ABCD-A1B1C1D1的棱长为1,点P,Q,R分别是棱A1A,A1B1,A1D1的中点,以△PQR为底面作正三棱柱.若此三棱柱另一底面的三个顶点也都在该正方体的表面上,则这个正三棱柱的高h=$\frac{\sqrt{3}}{2}$.
正方体ABCD-A1B1C1D1的棱长为1,点P,Q,R分别是棱A1A,A1B1,A1D1的中点,以△PQR为底面作正三棱柱.若此三棱柱另一底面的三个顶点也都在该正方体的表面上,则这个正三棱柱的高h=$\frac{\sqrt{3}}{2}$.