题目内容
5.函数f(x)是定义在(0,+∞)上的单调函数,?x∈(0,+∞),f[f(x)-lnx]=e+1,给出下面四个命题:①不等式f(x)>0恒成立;
②函数f(x)存在唯一零点x0,且x0∈(0,1);
③方程f(x)=x有且仅有一个根;
④方程f(x)-f′(x)=e+1(其中e为自然对数的底数)有唯一解x0,且x0∈(1,2).
其中正确命题的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 利用换元法求出函数f(x)的解析式,然后根据函数与方程的关系进行转化,构造函数,判断函数的零点即可得到结论.
解答 解:对于①∵f(x)是定义在(0,+∞)上单调函数,且对?x∈(0,+∞),都有f(f(x)-lnx)=e+1,
∴设f(x)-lnx=t,则f(t)=e+1,
即f(x)=lnx+t,
令x=t,则f(t)=lnt+t=e+1,
则t=e,
∴f(x)=lnx+e,
当f(x)>0时,即lnx+e>0,即-lnx<e,即ln$\frac{1}{x}$<lnee,解得x>$\frac{1}{{e}^{e}}$,故①错误;
对于②∵函数f(x)是定义在(0,+∞)上的单调函数,
f(0)<0,f(1)=e>0,
∴f(0)f(1)<0,
∴函数f(x)存在唯一零点x0,且x0∈(0,1);故②正确;
对于③∵f(x)=x,
∴lnx+e=x,
设g(x)=lnx+e-x,
∴g′(x)=$\frac{1}{x}$-1=$\frac{1-x}{x}$,
∴g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
当x=1时,g(x)max=g(1)=e-1>0,
∴g(x)=lnx+e-x在(1,+∞)上有两个零点,
∴方程f(x)=x有且两个根;故③错误;
对于④∵f′(x)=$\frac{1}{x}$>0,
则由f(x)-f′(x)=e+1得lnx+e-$\frac{1}{x}$=e+1,
即lnx-$\frac{1}{x}$-1=0,
设h(x)=lnx-$\frac{1}{x}$-1,
∵h(x)在(0,+∞)单调递增,
则h(3)=ln3-$\frac{1}{3}$-1<0,h(4)=ln4-$\frac{1}{4}$-1>0,
∴函数h(x)在(3,4)上存在一个零点,即方程f(x)-f′(x)=e+1的实数解所在的区间是(3,4);故④错误
故选:A.
点评 本题主要考查函数与方程的应用,根据函数单调性的性质,利用换元法求出函数的解析式是解决本题的关键.综合性较强,涉及的知识点较多.

 科学实验活动册系列答案
科学实验活动册系列答案| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{8}$ | D. | $\frac{2}{3}$ |
| A. | $\frac{1}{5}$ | B. | $\frac{2}{7}$ | C. | $\frac{2}{9}$ | D. | $\frac{9}{10}$ |
| A. | $\frac{3}{61}$ | B. | $\frac{2}{61}$ | C. | $\frac{1}{63}$ | D. | $\frac{1}{64}$ |
| A. | {1} | B. | {1,2} | C. | {2,3} | D. | {3} |
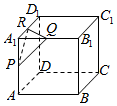 正方体ABCD-A1B1C1D1的棱长为1,点P,Q,R分别是棱A1A,A1B1,A1D1的中点,以△PQR为底面作正三棱柱.若此三棱柱另一底面的三个顶点也都在该正方体的表面上,则这个正三棱柱的高h=$\frac{\sqrt{3}}{2}$.
正方体ABCD-A1B1C1D1的棱长为1,点P,Q,R分别是棱A1A,A1B1,A1D1的中点,以△PQR为底面作正三棱柱.若此三棱柱另一底面的三个顶点也都在该正方体的表面上,则这个正三棱柱的高h=$\frac{\sqrt{3}}{2}$.