题目内容
8.已知函数f(x)=$\left\{\begin{array}{l}{-x,x≤0}\\{-{x}^{2}+2x,x>0}\end{array}\right.$,方程f2(x)-bf(x)=0,b∈(0,1),则方程的根的个数是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 化简可得f(x)=0或f(x)=b,作函数f(x)=$\left\{\begin{array}{l}{-x,x≤0}\\{-{x}^{2}+2x,x>0}\end{array}\right.$的图象,从而可得f(x)=0有两个不同的根,f(x)=b,(0<b<1)有三个不同的根;从而得到.
解答 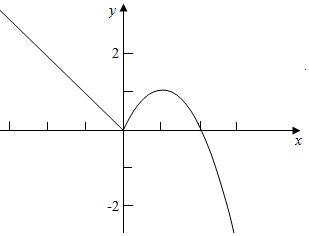 解:∵f2(x)-bf(x)=0,
解:∵f2(x)-bf(x)=0,
∴f(x)=0或f(x)=b,
作函数f(x)=$\left\{\begin{array}{l}{-x,x≤0}\\{-{x}^{2}+2x,x>0}\end{array}\right.$的图象如下,
,
结合图象可知,
f(x)=0有两个不同的根,f(x)=b,(0<b<1)有三个不同的根;
且5个根都不相同;
故方程的根的个数是5,
故选D.
点评 本题考查了方程的根与函数的零点的关系应用及分类讨论与数形结合的思想应用.

练习册系列答案
相关题目
20.学校开展运动会活动,甲、乙两同学各自报名参加跳高、跳远、游泳三个项目中的一个,每位同学参加每个项目的可能性相同,则这两位同学参加同一个体育项目的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{8}$ | D. | $\frac{2}{3}$ |
18.为了促进公民通过“走步”健身,中国平安公司推出的“平安好医生”软件,最近开展了“步步夺金”活动.活动规则:①使用平安好医生APP计步器,每天走路前1000步奖励0.3元红包,之后每2000步奖励0.1元红包,每天最高奖励不超过3元红包.②活动期间,连续3天领钱成功,从第4天起走路奖金翻1倍(乘以2),每天最高奖励不超过6元红包.某人连续使用此软件五天,并且每天领钱成功.这五天他走的步数统计如下:
则他第二天获得的奖励红包为1.0元,这五天累计获得的奖励红包为8.0元.
| 时间 | 第一天 | 第二天 | 第三天 | 第四天 | 第五天 |
| 步数 | 13980 | 15456 | 17890 | 19012 | 21009 |
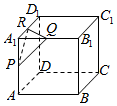 正方体ABCD-A1B1C1D1的棱长为1,点P,Q,R分别是棱A1A,A1B1,A1D1的中点,以△PQR为底面作正三棱柱.若此三棱柱另一底面的三个顶点也都在该正方体的表面上,则这个正三棱柱的高h=$\frac{\sqrt{3}}{2}$.
正方体ABCD-A1B1C1D1的棱长为1,点P,Q,R分别是棱A1A,A1B1,A1D1的中点,以△PQR为底面作正三棱柱.若此三棱柱另一底面的三个顶点也都在该正方体的表面上,则这个正三棱柱的高h=$\frac{\sqrt{3}}{2}$.