题目内容
1.若$\overrightarrow{a}$与$\overrightarrow{b}$是非零向量,且|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,则$\overrightarrow{a}$的方向与$\overrightarrow{a}$+$\overrightarrow{b}$的方向所成的角是( )| A. | 0° | B. | 60° | C. | 30° | D. | 45° |
分析 根据向量的几何意义,设$\overrightarrow{a}$=$\overrightarrow{OA}$,$\overrightarrow{b}$=$\overrightarrow{OB}$,由|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,得到△OAB为等边三角形,容易判断$\overrightarrow{a}$的方向与$\overrightarrow{a}$+$\overrightarrow{b}$的方向所成的角.
解答 解:设$\overrightarrow{a}$=$\overrightarrow{OA}$,$\overrightarrow{b}$=$\overrightarrow{OB}$,由|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,
得到△OAB为等边三角形,
所以$\overrightarrow{a}$的方向与$\overrightarrow{a}$+$\overrightarrow{b}$的方向所成的角是30°;
故选C.
点评 本题考查了平面向量的模长以及夹角;利用几何意义解答是关键.

练习册系列答案
相关题目
9.若函数y=f(x)在区间(a,b)内可导,且x0∈(a,b)则$\lim_{h→0}\frac{{f({x_0}-h)\;-f({x_0})}}{h}$的值为( )
| A. | f′(x0) | B. | -f′(x0) | C. | -2f′(x0) | D. | 0 |
10.宁夏2011年起每年举办一届旅游节,到2016年已举办了六届,旅游部门统计在每届旅游节期间,吸引了不少外地游客到宁夏,这将极大地推进宁夏的旅游业的发展,现将前五届旅游节期间外地游客到宁夏的人数统计如下表:
(1)求y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$
(2)利用(1)中的线性回归方程,预测17年第7届旅游节期间外地游客到宁夏的人数.
| 年份 | 11年 | 12年 | 13年 | 14年 | 15年 |
| 旅游节届编号x | 1 | 2 | 3 | 4 | 5 |
| 外地游客人数y(单位:十万) | 0.6 | 0.8 | 0.9 | 1.2 | 1.5 |
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$
(2)利用(1)中的线性回归方程,预测17年第7届旅游节期间外地游客到宁夏的人数.
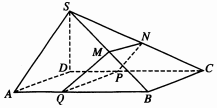 已知四棱锥S-ABCD的底面为平行四边形,且SD⊥平面ABCD,AB=2AD=2SD,∠DCB=60°,M,N分别为SB,SC的中点,过MN作平面MNPQ分别与线段CD,AB相交于P,Q两点(不与A,B重合).
已知四棱锥S-ABCD的底面为平行四边形,且SD⊥平面ABCD,AB=2AD=2SD,∠DCB=60°,M,N分别为SB,SC的中点,过MN作平面MNPQ分别与线段CD,AB相交于P,Q两点(不与A,B重合).