题目内容
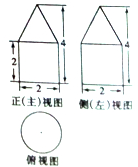
已知某几何体的三视图如图所示，则该几何体的体积为（ ）
A、
| ||
| B、3π | ||
C、
| ||
| D、6π |
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：几何体是圆柱与圆锥的组合体，根据三视图判断圆柱与圆锥的底面半径和高，把数据代入圆柱与圆锥的体积公式计算．
解答：
解：由三视图知：几何体是圆柱与圆锥的组合体，
其中圆柱与圆锥的底面半径都是1，高都为2，
∴几何体的体积V=π×12×2+
×π×12×2=2π+
=
．
故选：A．
其中圆柱与圆锥的底面半径都是1，高都为2，
∴几何体的体积V=π×12×2+
| 1 |
| 3 |
| 2π |
| 3 |
| 8π |
| 3 |
故选：A．
点评：本题考查了由三视图求几何体的体积，根据三视图判断几何体的形状及数据所对应的几何量是关键．
练习册系列答案
相关题目
幂函数y=xa，当a取不同的正数时，在区间[0，1]上它们的图象是一族美丽的曲线（如图），设点A（1，0）、B（0，1），若y=xα，y=xβ的图象与线段AB分别交于M、N，且| (1+i)3 |
| (1-i)2 |
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
设
，
为非零向量，|
|=2|
|，两组向量
，
，
，
和
，
，
，
，均由2个
和2个
排列而成，若
•
+
•
+
•
+
•
所有可能取值中的最小值为4|
|2，则
与
的夹角为（ ）
| a |
| b |
| b |
| a |
| x1 |
| x2 |
| x3 |
| x4 |
| y1 |
| y2 |
| y3 |
| y4 |
| a |
| b |
| x1 |
| y1 |
| x2 |
| y2 |
| x3 |
| y3 |
| x4 |
| y4 |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
| D、0 |
已知复数z满足（3-4i）z=25，则z=（ ）
| A、-3-4i | B、-3+4i |
| C、3-4i | D、3+4i |
i是虚数单位，复数
=（ ）
| 7+i |
| 3+4i |
| A、1-i | ||||
| B、-1+i | ||||
C、
| ||||
D、-
|
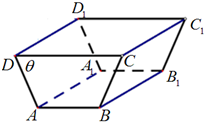某农户准备建一个水平放置的直四棱柱形储水窖（如图），其中直四棱柱的高AA1=10m，两底面ABCD，A1B1C1D1是高为2m，面积为10m2的等腰梯形，且∠ADC=θ（0＜θ＜