题目内容
8.设A为某圆周上一定点,在圆周上任取一点P,则弦长|AP|超过半径的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{π}$ | D. | 1-$\frac{1}{π}$ |
分析 当弦长|AP|等于半径时△OAP为等边三角形,所以弦长|AP|超过半径的P的位置在240°的优弧上,由几何概型的公式得到所求.
解答 解:设A为某圆周上一定点,在圆周上任取一点P,当弦长|AP|等于半径时△OAP为等边三角形,
所以弦长|AP|超过半径的P的位置在240°的优弧上,由几何概型得到$\frac{240}{360}=\frac{2}{3}$;
故选B.
点评 本题考查了几何概型的概率求法;关键是明确几何测度为角度,利用角度比求概率.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
18.某地区根据2008年至2014年每年的生活垃圾无害化处理量y(单位:万吨)的数据,用线性回归模型拟合y关于t的回归方程为$\widehat{y}$=0.92+0.1t(t表示年份代码,自2008年起,t的取值分别为1,2,3,…),则下列的表述正确的是( )
| A. | 自2008年起,每年的生活垃圾无害化处理量与年份代码负相关 | |
| B. | 自2008年起,每年的生活垃圾无害化处理量大约增加0.92万吨 | |
| C. | 由此模型预测出2017年该地区的生活垃圾无害化处理量约1.92万吨 | |
| D. | 由此模型预测出2017年该地区的生活垃圾无害化处理量约1.82万吨 |
19.已知α是第三象限角.且sinα=-$\frac{1}{3}$,则3cosα+4tanα=( )
| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | -$\sqrt{3}$ | D. | $\sqrt{3}$ |
20. 如图,在边长为a的正方形内有图形Ω,现向正方形内撒豆子,若撒在图形Ω内核正方形内的豆子数分别为m,n,则图形Ω面积的估计值为( )
如图,在边长为a的正方形内有图形Ω,现向正方形内撒豆子,若撒在图形Ω内核正方形内的豆子数分别为m,n,则图形Ω面积的估计值为( )
 如图,在边长为a的正方形内有图形Ω,现向正方形内撒豆子,若撒在图形Ω内核正方形内的豆子数分别为m,n,则图形Ω面积的估计值为( )
如图,在边长为a的正方形内有图形Ω,现向正方形内撒豆子,若撒在图形Ω内核正方形内的豆子数分别为m,n,则图形Ω面积的估计值为( )| A. | $\frac{ma}{n}$ | B. | $\frac{na}{m}$ | C. | $\frac{m{a}^{2}}{n}$ | D. | $\frac{n{a}^{2}}{m}$ |
17.圆(x-1)2+(y-2)2=1上的动点P到直线3x-4y-10=0的距离的最小值为( )
| A. | 2 | B. | 1 | C. | 3 | D. | 4 |
18.函数f(x)=(x+1)2-2x的零点个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
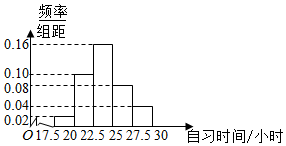 某高校为调查1000名学生每周的自习时间(单位:小时),从中随机抽查了100名学生每周的自习时间,制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,估计这1000名学生中每周的自习时间不少于22.5小时的人数是700.
某高校为调查1000名学生每周的自习时间(单位:小时),从中随机抽查了100名学生每周的自习时间,制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,估计这1000名学生中每周的自习时间不少于22.5小时的人数是700.