题目内容
1.在△ABC中,a=$\sqrt{3}$,b=1,∠A=$\frac{π}{3}$,则cosB=$\frac{\sqrt{3}}{2}$.分析 由已知利用正弦定理可求sinB,利用大边对大角可求B为锐角,利用同角三角函数基本关系式可求cosB的值.
解答 解:∵a=$\sqrt{3}$,b=1,∠A=$\frac{π}{3}$,
∴由正弦定理可得:sinB=$\frac{bsinA}{a}$=$\frac{1×\frac{\sqrt{3}}{2}}{\sqrt{3}}$=$\frac{1}{2}$,
∵b<a,B为锐角,
∴cosB=$\sqrt{1-si{n}^{2}B}$=$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题主要考查了正弦定理,大边对大角,同角三角函数基本关系式在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
16.设i是虚数单位,则复数i3-$\frac{2}{i}$=( )
| A. | i | B. | 3i | C. | -i | D. | -3i |
6.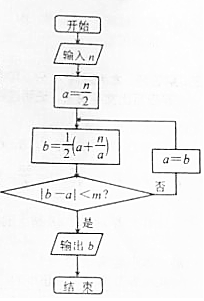 一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的n为6时,输出结果为2.45,则m可以是( )
一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的n为6时,输出结果为2.45,则m可以是( )
 一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的n为6时,输出结果为2.45,则m可以是( )
一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的n为6时,输出结果为2.45,则m可以是( )| A. | 0.6 | B. | 0.1 | C. | 0.01 | D. | 0.05 |
13.设变量x,y满足线性约束条件$\left\{\begin{array}{l}{x+y≤1}\\{x-y≤1}\\{x≥0}\end{array}\right.$,则z=x+2y的最小值为( )
| A. | -2 | B. | -1 | C. | 2 | D. | 1 |
10.已知集合M={x|x2≤1},N={x|log2x<1},则M∩N=( )
| A. | [-1,2) | B. | [-1,1] | C. | (0,1] | D. | (-∞,2) |
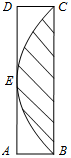 如图所示矩形ABCD边长AB=1,AD=4,抛物线顶点为边AD的中点E,且B,C两点在抛物线上,则从矩形内任取一点落在抛物线与边BC围成的封闭区域(包含边界上的点)内的概率是$\frac{2}{3}$.
如图所示矩形ABCD边长AB=1,AD=4,抛物线顶点为边AD的中点E,且B,C两点在抛物线上,则从矩形内任取一点落在抛物线与边BC围成的封闭区域(包含边界上的点)内的概率是$\frac{2}{3}$.