题目内容
17.如图,在△ABC中,D,E是BC上的两个三等分点,若$\overrightarrow{AB}$•$\overrightarrow{AC}$=2,$\overrightarrow{AD}$•$\overrightarrow{AE}$=4,则BC的长度为3.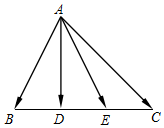
分析 由已知求出${\overrightarrow{AB}}^{2}+{\overrightarrow{AC}}^{2}$,然后由$\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$求解$|\overrightarrow{BC}{|}^{2}$,则答案可求.
解答 解:∵$\overrightarrow{AB}$•$\overrightarrow{AC}$=2,
且$\overrightarrow{AD}$•$\overrightarrow{AE}$=$(\overrightarrow{AB}+\overrightarrow{BD})•(\overrightarrow{AC}+\overrightarrow{CE})$=$(\overrightarrow{AB}+\frac{1}{3}\overrightarrow{BC})•(\overrightarrow{AC}-\frac{1}{3}\overrightarrow{BC})$
=$(\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC})•(\frac{2}{3}\overrightarrow{AC}+\frac{1}{3}\overrightarrow{AB})$=$\frac{5}{9}\overrightarrow{AB}•\overrightarrow{AC}+\frac{2}{9}({\overrightarrow{AB}}^{2}+{\overrightarrow{AC}}^{2})=4$,
得$\frac{10}{9}+\frac{2}{9}({\overrightarrow{AB}}^{2}+{\overrightarrow{AC}}^{2})=4$,
∴${\overrightarrow{AB}}^{2}+{\overrightarrow{AC}}^{2}=13$.
∴$|\overrightarrow{BC}{|}^{2}=(\overrightarrow{AC}-\overrightarrow{AB})^{2}={\overrightarrow{AB}}^{2}+{\overrightarrow{AC}}^{2}-2\overrightarrow{AB}•\overrightarrow{AC}$=13-4=9.
∴$|\overrightarrow{BC}|=3$.
故答案为:3.
点评 本题考查平面向量的数量积运算,考查了数学转化思想方法,是中档题.

| A. | {-1,0,1} | B. | {1} | C. | {0,1} | D. | {-1,0} |
| 节气 | 冬至 | 小寒 (大雪) | 大寒 (小雪) | 立春 (立冬) | 雨水 (霜降) | 惊蛰 (寒露) | 春分 (秋分) | 清明 (白露) | 谷雨 (处暑) | 立夏 (立秋) | 小满 (大暑) | 芒种 (小暑) | 夏至 |
| 晷影长 (寸) | 135 | 125$\frac{5}{6}$ | 115.1$\frac{4}{6}$ | 105.2$\frac{4}{6}$ | 95.3$\frac{2}{6}$ | $85.4\frac{2}{6}$ | 75.5 | 66.5$\frac{5}{6}$ | $55.6\frac{4}{6}$ | 45.7$\frac{3}{6}$ | 35.8$\frac{2}{6}$ | 25.9$\frac{1}{6}$ | 16.0 |
| A. | 72.4寸 | B. | 81.4寸 | C. | 82.0寸 | D. | 91.6寸 |
| A. | 若a>b,则a-c>b-c | B. | 若a>b,则$\frac{1}{a}<\frac{1}{b}$ | C. | 若a>b,则a2>b2 | D. | 若a>b,则ac2>bc2 |
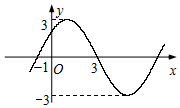 函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ∈[0,2π))的图象,如图所示,则f(2016)的值为$\frac{{3\sqrt{2}}}{2}$.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ∈[0,2π))的图象,如图所示,则f(2016)的值为$\frac{{3\sqrt{2}}}{2}$.