题目内容
20. 如图,在平行四边形OABC中,O为坐标原点,过点C(1,3)作CD⊥AB于点D,
如图,在平行四边形OABC中,O为坐标原点,过点C(1,3)作CD⊥AB于点D,(1)求CD所在直线的方程;
(2)当D(4,2)时,求△OCD外接圆的方程.
分析 (1)根据题意,由直线的斜率公式可得KOC,进而可得CD所在直线的斜率为KCD,由直线的点斜式方程计算可得答案;
(2)设△OCD外接圆方程为(x-a)2+(y-b)2=r2,由圆所过点的坐标可得$\left\{\begin{array}{l}{{a}^{2}+{b}^{2}={r}^{2}}\\{(1-a)^{2}+(3-b)^{2}={r}^{2}}\\{(4-a)^{2}+(2-b)^{2}={r}^{2}}\end{array}\right.$,解可得a、b、r2的值,将其代入圆的标准方程即可得答案.
解答 解:(1)根据题意,∵点O(0,0),点C(1,3),
∴OC所在直线的斜率为KOC=$\frac{3-0}{1-0}$=3.
在平行四边形OABC中,AB∥OC,
∵CD⊥AB,∴CD⊥OC.∴CD所在直线的斜率为KCD=-$\frac{1}{3}$,
∴CD所在直线方程为y-3=-$\frac{1}{3}$(x-1),即x+3y-10=0;
(2)设△OCD外接圆方程为(x-a)2+(y-b)2=r2,
圆过O(0,0)、C(1,3)、D(4,2),
则有$\left\{\begin{array}{l}{{a}^{2}+{b}^{2}={r}^{2}}\\{(1-a)^{2}+(3-b)^{2}={r}^{2}}\\{(4-a)^{2}+(2-b)^{2}={r}^{2}}\end{array}\right.$,
解可得a=2,b=1,r2=5,
故所求圆方程:(x-2)2+(y-1)2=5.
点评 本题考查直线的方程与圆的标准方程求法,注意直线的平行与垂直和直线的斜率的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.函数y=sin3x在($\frac{π}{3}$,0)处的切线斜率为( )
| A. | -1 | B. | 1 | C. | -3 | D. | 3 |
15.已知等差数列{an}的前n项和为Sn,a5=10,且S6+3a7=S8+12,则公差d等于( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
9.设集合U={0,1,2,3,4,5},M={1,4,5},N={0,3,5},则M∩(∁UN)=( )
| A. | {1} | B. | {1,4} | C. | {1,4,5} | D. | {1,2,4,5} |
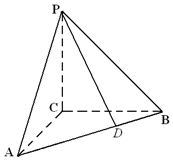 如图,在三棱锥P-ABC中,PC⊥平面ABC,PC=4,AC=BC=3,∠ACB=90°.点D在线段AB上,AD=2DB.
如图,在三棱锥P-ABC中,PC⊥平面ABC,PC=4,AC=BC=3,∠ACB=90°.点D在线段AB上,AD=2DB.