题目内容
设F1,F2是椭圆
+
=1的两个焦点,P是椭圆上的点,且|PF1|:|PF2|=4:3,则△PF1F2的面积为 .
| 4x2 |
| 49 |
| y2 |
| 6 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据椭圆方程,得a=
,b=
,c=2.5.得椭圆的焦点为F1(-2.5,0),F2(2.5,0),由椭圆的定义结合|PF1|:|PF2|=4:3,得|PF1|=4,|PF2|=3,结合勾股定理的逆定理得△PF1F2是以P为直角顶点的直角三角形,由此不难得到△PF1F2的面积.
| 7 |
| 2 |
| 6 |
解答:
解:∵椭圆的方程为
+
=1,
∴a=
,b=
,c=2.5.
得椭圆的焦点为F1(-2.5,0),F2(2.5,0),
∵|PF1|+|PF2|=2a=7,且|PF1|:|PF2|=4:3,
∴|PF1|=4,|PF2|=3,
可得|PF1|2+|PF2|2=25=|F1F2|2,
因此,△PF1F2是以P为直角顶点的直角三角形,
得△PF1F2的面积S=
|PF1|•|PF2|=6
故答案为:6.
| 4x2 |
| 49 |
| y2 |
| 6 |
∴a=
| 7 |
| 2 |
| 6 |
得椭圆的焦点为F1(-2.5,0),F2(2.5,0),
∵|PF1|+|PF2|=2a=7,且|PF1|:|PF2|=4:3,
∴|PF1|=4,|PF2|=3,
可得|PF1|2+|PF2|2=25=|F1F2|2,
因此,△PF1F2是以P为直角顶点的直角三角形,
得△PF1F2的面积S=
| 1 |
| 2 |
故答案为:6.
点评:本题给出椭圆的两条焦半径的比值,求焦点三角形的面积,着重考查了椭圆的标准方程与简单几何性质等知识,属于中档题.

练习册系列答案
相关题目
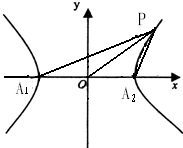 如图,P是双曲线
如图,P是双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、(0,
| ||
B、(0,
| ||
C、(0,
| ||
D、(0,
|
已知A,B是两个相互独立事件,P(A),P(B)分别表示它们发生的概率,则1-P(A)P(B)是下列哪个事件的概率( )
| A、事件A,B同时发生 |
| B、事件A,B至少有一个发生 |
| C、事件A,B至多有一个发生 |
| D、事件A,B都不发生 |
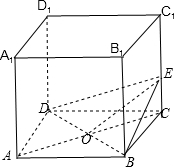 如图,正方体ABCD-A1B1C1D1,边长为1,E为CC1上一点,且EC=
如图,正方体ABCD-A1B1C1D1,边长为1,E为CC1上一点,且EC=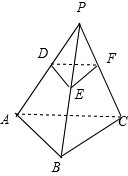 如图,已知点P为△ABC所在平面外任一点点D、E、F分别在射线PA、PB、PC上并且
如图,已知点P为△ABC所在平面外任一点点D、E、F分别在射线PA、PB、PC上并且