题目内容
已知动点P到直线l:x+4=0的距离与它到点M(2,0)的距离之差为2,记点P的轨迹为曲线C.
(Ⅰ)求曲线C的方程;
(Ⅱ)问直线l上是否存在点Q,使得过点Q且斜率分别为k1,k2的两直线与曲线C相切,同时满足k1+2k2=0,若存在,求出点Q的坐标;若不存在,请说明理由.
(Ⅰ)求曲线C的方程;
(Ⅱ)问直线l上是否存在点Q,使得过点Q且斜率分别为k1,k2的两直线与曲线C相切,同时满足k1+2k2=0,若存在,求出点Q的坐标;若不存在,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)根据抛物线定义,曲线C是以(2,0)为焦点,x=-2为准线的抛物线,由此能求出曲线C的方程.
(Ⅱ)设Q(-4,y0),过Q与C相切的直线设为y-y0=k(x+4),k≠0,联立
,得ky2-8y+8y0+32k=0,由此能求出存在点Q(-4,2)和(-4,-2),使得过点Q的两直线与曲线C相切,且满足k1+2k2=0.
(Ⅱ)设Q(-4,y0),过Q与C相切的直线设为y-y0=k(x+4),k≠0,联立
|
解答:
解:(Ⅰ)根据抛物线定义,曲线C是以(2,0)为焦点,x=-2为准线的抛物线,
∴p=4,
∴曲线C的方程为y2=8x.
(Ⅱ)设Q(-4,y0),过Q与C相切的直线设为y-y0=k(x+4),k≠0,
联立
,得ky2-8y+8y0+32k=0,
∵直线与曲线C相切,
∴△=64-4k(8y0+32k)=0,∴4k2+y0k-2=0,
∴
,
∵k1,k2是两切线的斜率,且满足k1+2k2=0,
∴k1=-
,k2=
,又∵k1k2=-
,∴y0=±2,
∴存在点Q(-4,2)和(-4,-2),使得过点Q的两直线与曲线C相切,且满足k1+2k2=0.
∴p=4,
∴曲线C的方程为y2=8x.
(Ⅱ)设Q(-4,y0),过Q与C相切的直线设为y-y0=k(x+4),k≠0,
联立
|
∵直线与曲线C相切,
∴△=64-4k(8y0+32k)=0,∴4k2+y0k-2=0,
∴
|
∵k1,k2是两切线的斜率,且满足k1+2k2=0,
∴k1=-
| y0 |
| 2 |
| y0 |
| 4 |
| 1 |
| 2 |
∴存在点Q(-4,2)和(-4,-2),使得过点Q的两直线与曲线C相切,且满足k1+2k2=0.
点评:本题考查曲线方程的求法,考查满足条件的点是否存在的判断与求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
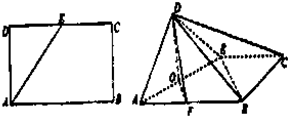 已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△ADE折起,使平面ADE上平面ABCE,点O、F分别是AE、AB的中点.
已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△ADE折起,使平面ADE上平面ABCE,点O、F分别是AE、AB的中点.