题目内容
已知直线l过点(0,4),取直线l上的一点P作圆C:x2+y2-2y=0的切线PA、PB(A、B为切点),若四边形PACB的面积的最小值为2,则直线l的斜率k为 .
考点:直线与圆的位置关系
专题:直线与圆
分析:由圆的方程为求得圆心C,半径r,由“若四边形面积最小,则圆心与点P的距离最小时,即距离为圆心到直线的距离时,切线长PA,PB最小”,最后利用点到直线的距离求出直线的斜率即可..
解答:
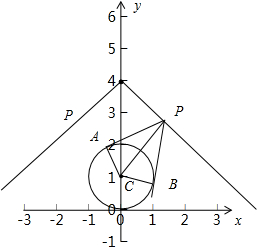 解:∵圆的方程为:x2+(y-1)2=1,
解:∵圆的方程为:x2+(y-1)2=1,
∴圆心C(0,1),半径r=1.
根据题意,若四边形面积最小,当圆心与点P的距离最小时,即距离为圆心到直线l的距离最小时,
切线长PA,PB最小.切线长为2,
∴PA=PB═2,
∴圆心到直线l的距离为d=
.直线方程为y-4=kx,即kx-y+4=0,
∴
=
,解得k=±
,
所求直线的斜率为:±
.
故答案为:±
.
 解:∵圆的方程为:x2+(y-1)2=1,
解:∵圆的方程为:x2+(y-1)2=1,∴圆心C(0,1),半径r=1.
根据题意,若四边形面积最小,当圆心与点P的距离最小时,即距离为圆心到直线l的距离最小时,
切线长PA,PB最小.切线长为2,
∴PA=PB═2,
∴圆心到直线l的距离为d=
| 5 |
∴
| 5 |
| |4-1| | ||
|
2
| ||
| 5 |
所求直线的斜率为:±
2
| ||
| 5 |
故答案为:±
2
| ||
| 5 |
点评:本题的考点是直线与圆的位置关系,主要涉及了构造四边形及其面积的求法,解题的关键是“若四边形面积最小,则圆心与点P的距离最小时,即距离为圆心到直线的距离时,切线长PA,PB最小”属于中档题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
已知α:“a=2”;β:“直线x-y=0与圆x2+(y-a)2=2相切”.则α是β的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分也非必要条件 |