题目内容
已知函数f(x)=
,下列关于函数g(x)=[f(x)]2+af(x)-1(其中a为常数)的叙述中:
①对?a∈R,函数g(x)至少有一个零点;
②当a=0时,函数g(x)有两个不同零点;
③?a∈R,使得函数g(x)有三个不同零点;
④函数g(x)有四个不同零点的充要条件是a<0.
其中真命题有 .(把你认为的真命题的序号都填上)
|
①对?a∈R,函数g(x)至少有一个零点;
②当a=0时,函数g(x)有两个不同零点;
③?a∈R,使得函数g(x)有三个不同零点;
④函数g(x)有四个不同零点的充要条件是a<0.
其中真命题有
考点:命题的真假判断与应用,函数零点的判定定理
专题:数形结合,函数的性质及应用
分析:首先化简函数式,结合指数函数的性质、基本不等式,求出函数的值域,画出函数f(x)的图象,对g(x)=0的两根加以判断,通过a的取值,结合图象一一加以判断即可.
解答:
 解:当0≤x≤1时,f(x)=2x-1-1=2x-2,当x<0时,f(x)=1-2x-1=-2x,且-1≤f(x)≤0,
解:当0≤x≤1时,f(x)=2x-1-1=2x-2,当x<0时,f(x)=1-2x-1=-2x,且-1≤f(x)≤0,
当x>1时,f(x)=
=x-1+
-1,
且f(x)≥1,如右图所示,
又函数g(x)=[f(x)]2+af(x)-1(其中a为常数)
判别式为a2+4>0,则g(x)=0有两个不等的实根,且
设f(x)=m,n,且mn=-1,m+n=-a,
①若a=
,则设m=-2,n=
,则结合图象可知,
函数g(x)没有零点,故①错;
②当a=0时,g(x)=0则f(x)=±1,函数g(x)有两个零点,故②正确;
③若存在函数g(x)有三个不同零点,则x轴上方2个,下方1个;或上方1个,下方2个.即有f(x)=-1,
由于mn=-1,故还有f(x)=1,不成立;第二种情况也不成立,上方有1个,即f(x)=1,还有f(x)=-1,
故③错;
④函数g(x)有四个不同零点?即在x轴上方有两个、下方有两个,即-1<m<0且n>1,即m+n>0,-a>0
即a<0,故函数g(x)有四个不同零点的充要条件是a<0,即④正确.
故答案为:②④.
 解:当0≤x≤1时,f(x)=2x-1-1=2x-2,当x<0时,f(x)=1-2x-1=-2x,且-1≤f(x)≤0,
解:当0≤x≤1时,f(x)=2x-1-1=2x-2,当x<0时,f(x)=1-2x-1=-2x,且-1≤f(x)≤0,当x>1时,f(x)=
| (x-1)2+2-x |
| x-1 |
| 1 |
| x-1 |
且f(x)≥1,如右图所示,
又函数g(x)=[f(x)]2+af(x)-1(其中a为常数)
判别式为a2+4>0,则g(x)=0有两个不等的实根,且
设f(x)=m,n,且mn=-1,m+n=-a,
①若a=
| 3 |
| 2 |
| 1 |
| 2 |
函数g(x)没有零点,故①错;
②当a=0时,g(x)=0则f(x)=±1,函数g(x)有两个零点,故②正确;
③若存在函数g(x)有三个不同零点,则x轴上方2个,下方1个;或上方1个,下方2个.即有f(x)=-1,
由于mn=-1,故还有f(x)=1,不成立;第二种情况也不成立,上方有1个,即f(x)=1,还有f(x)=-1,
故③错;
④函数g(x)有四个不同零点?即在x轴上方有两个、下方有两个,即-1<m<0且n>1,即m+n>0,-a>0
即a<0,故函数g(x)有四个不同零点的充要条件是a<0,即④正确.
故答案为:②④.
点评:本题主要考查函数的零点及判断,考查函数的性质及运用,考查数形结合的思想方法,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
双曲线x2-
=1的右焦点到准线的距离为( )
| y2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
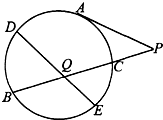 如图,PA为圆的切线,切点为A,割线PCB与圆相交于B、C两点,弦DE经过弦BC的中点Q,若AP=3
如图,PA为圆的切线,切点为A,割线PCB与圆相交于B、C两点,弦DE经过弦BC的中点Q,若AP=3