题目内容
10.已知数列{an}满足a1=$\frac{1}{3}$,an+1=$\frac{{a}_{n}}{2{a}_{n}+1}$(n∈N*),则$\frac{{a}_{3}+{a}_{1005}}{{a}_{3}{a}_{1005}}$=( )| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
分析 a1=$\frac{1}{3}$,an+1=$\frac{{a}_{n}}{2{a}_{n}+1}$(n∈N*),取倒数可得:$\frac{1}{{a}_{n+1}}-\frac{1}{{a}_{n}}$=2,利用等差数列的通项公式即可得出.
解答 解:∵a1=$\frac{1}{3}$,an+1=$\frac{{a}_{n}}{2{a}_{n}+1}$(n∈N*),
∴$\frac{1}{{a}_{n+1}}-\frac{1}{{a}_{n}}$=2,
∴数列$\{\frac{1}{{a}_{n}}\}$是等差数列,首项为3,公差为2.
∴$\frac{1}{{a}_{n}}$=3+2(n-1)=2n+1,
则$\frac{{a}_{3}+{a}_{1005}}{{a}_{3}{a}_{1005}}$=$\frac{1}{{a}_{3}}+\frac{1}{{a}_{1005}}$=7+2×1005+1=2018.
故选:D.
点评 本题考查了等差数列的通项公式、“取倒数”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
7.如图,正六边形ABCDEF中,$\overrightarrow{BC}$$+\overrightarrow{DE}$$+\overrightarrow{AF}$等于( )
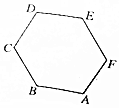

| A. | $\overrightarrow{EB}$ | B. | $\overrightarrow{BE}$ | C. | $\overrightarrow{AD}$ | D. | $\overrightarrow{CF}$ |
15.设x,y满足约束条件$\left\{\begin{array}{l}x+y≤3\\ x≥1\\ y≥1\end{array}\right.$,则$z=\frac{y}{x}$的最大值为 ( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
2.某校高二年级共有24个班,为了解该年级学生对数学的喜爱程度,将每个班编号,依次为1到24,现用系统抽样方法抽取4个班进行调查,若抽到的编号之和为52,则抽取的最小编号是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
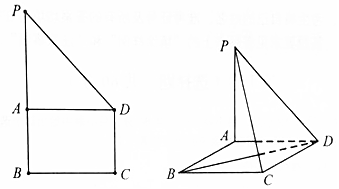 如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,点A在边PB上,AD∥BC,PB=3BC=6,现沿AD将△PAD折起,使平面PAD⊥平面ABCD.
如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,点A在边PB上,AD∥BC,PB=3BC=6,现沿AD将△PAD折起,使平面PAD⊥平面ABCD.