题目内容
20.在平面直角坐标系xoy中,直线y=2x+b是曲线y=2alnx的切线,则当a>0时,实数b的最小值是-2.分析 求出函数y的导数,设切点为(m,n),由条件得到2=$\frac{2a}{m}$,n=2m+b,n=2alnm,即有b=2alna-2a(a>0),再对b求导,求出单调区间,极值也为最值,即可得到所求.
解答 解:y=2alnx的导数为y′=$\frac{2a}{x}$,
由于直线y=2x+b是曲线y=2alnx的切线,
则设切点为(m,n),
则2=$\frac{2a}{m}$,n=2m+b,n=2alnm,
即有b=2alna-2a(a>0),
b′=2(lna+1)-2=2lna,
当a>1时,b′>0,函数b递增,
当0<a<1时,b′<0,函数b递减,即有a=1为极小值点,
也为最小值点,且最小值为:2ln1-2=-2.
故答案为:-2.
点评 本题考查导数的运用:求切线方程和求单调区间和极值、最值,考查运算能力,属于中档题.

练习册系列答案
相关题目
10.已知数列{an}满足a1=$\frac{1}{3}$,an+1=$\frac{{a}_{n}}{2{a}_{n}+1}$(n∈N*),则$\frac{{a}_{3}+{a}_{1005}}{{a}_{3}{a}_{1005}}$=( )
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
5.已知集合$A=\left\{{x|0≤x<1}\right\},B=\left\{{x|\frac{1}{x}≥1}\right\}$,则A∪B=( )
| A. | R | B. | [0,+∞) | C. | [0,1] | D. | (0,1) |
12.已知|x+2|+|6-x|≥k恒成立
(1)求实数k的最大值;
(2)若实数k的最大值为n,正数a,b满足$\frac{8}{5a+b}+\frac{2}{2a+3b}=n$,求7a+4b的最小值.
(1)求实数k的最大值;
(2)若实数k的最大值为n,正数a,b满足$\frac{8}{5a+b}+\frac{2}{2a+3b}=n$,求7a+4b的最小值.
9.设p:2x2-3x+1≤0,q:x2-(2a+1)x+a(a+1)≤0,若非p是非q的必要不充分条件,则实数a的取值范围是( )
| A. | (-∞,0)∪($\frac{1}{2}$,+∞) | B. | (-∞,0]∪[$\frac{1}{2}$,+∞) | C. | (0,$\frac{1}{2}$) | D. | [0,$\frac{1}{2}$] |
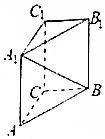 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=1,CC1=2,则异面直线A1B与AC所成角的余弦值是$\frac{\sqrt{6}}{6}$.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=1,CC1=2,则异面直线A1B与AC所成角的余弦值是$\frac{\sqrt{6}}{6}$.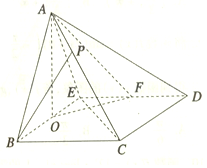 在四棱锥A-BCDE中,底面BCDE为菱形,侧面ABE为等边三角形,且侧面ABE⊥底面BCDE,O,F分别为BE,DE的中点,点P在AC上,且AP=$\frac{1}{3}$AC.
在四棱锥A-BCDE中,底面BCDE为菱形,侧面ABE为等边三角形,且侧面ABE⊥底面BCDE,O,F分别为BE,DE的中点,点P在AC上,且AP=$\frac{1}{3}$AC.