Question

已知函数f（x）=

x2

a

+bx-lnx．
（1）若a=b=1，求函数f（x）的单调性与极值；
（2）若b=-1，函数f（x）有且只有一个零点，求实数a的取值范围．

Answer 1

考点：利用导数研究函数的单调性,函数的零点,利用导数研究函数的极值

专题：计算题,转化思想,导数的综合应用

分析：（1）求出导数，分别令导数大于0，小于0，即可得到增区间和减区间，极值，注意定义域．
（2）利用参数分离将问题转化成

1

a

=

x+lnx

x2

有唯一正实数根，再通过求导的方式研究其性质，注意到函数的导函数比较复杂，因此在研究时，可将导函数分成分子，分母来分别研究．

解答： 解：（1）f（x）=x²+x-lnx，（x＞0），
f′（x）=2x+1-

1

x

=

(2x-1)(x+1)

x

，
当x＞

1

2

时，f′（x）＞0，f（x）递增，
当0＜x＜

1

2

时，f′（x）＜0，f（x）递减，
则函数f（x）的单调增区间为（

1

2

，+∞），
单调递减区间（0，

1

2

）．有极小值f（

1

2

）=

3

4

+ln2，无极大值；
（2）由f（x）=

x2

a

-x-lnx=0，即

1

a

=

x+lnx

x2

有唯一正实数根．
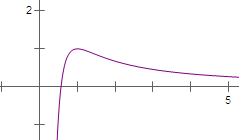
令g（x）=

x+lnx

x2

，即函数y=

1

a

与函数y=g（x）有唯一交点；
g′（x）=

x-x2-2xlnx

x4

=

1-x-2lnx

x3

，
再令R（x）=1-x-2lnx，R'（x）=-1-

2

x

，?x＞0，
且易得R（1）=0，
故当x∈（0，1）时，R（x）＞0，g′（x）＞0，函数g（x）单调递增；
当x∈（1，+∞）时，R（x）＜0，g′（x）＜0，函数g（x）单调递减；
即g（x）≤g（1）=1，
又当x→0时，g（x）→-∞，
而当x→+∞时，g（x）→0且g（x）＞0，
故满足条件的实数a的取值范围为：{a|a＜0，或a=1}．

点评：本题考查导数的运用：求单调区间和极值、最值，考查参数分离是恒成立问题中常用的技巧方法，值得一提的是在用导数的方法研究函数性质时，当所求的导函数形式比较复杂时，可以考虑分别去研究函数的性质，属于中档题．