题目内容
18.已知命题,若m>$\frac{1}{4}$,则mx2-x+1=0无实根,写出该命题的逆命题、否命题、逆否命题,并判断它们的真假.分析 根据四种命题的定义,可得该命题的逆命题、否命题、逆否命题,进而判断它们的真假.
解答 解:若m>$\frac{1}{4}$时,则方程为二次方程,且△=1-4m<0,为真命题,
其逆命题为:若mx2-x+1=0无实根,则m>$\frac{1}{4}$为真命题,
其否命题为:若m≤$\frac{1}{4}$,则mx2-x+1=0有实根为真命题,
其逆否命题为:若mx2-x+1=0有实根,则m≤$\frac{1}{4}$为真命题.
点评 本题以命题的真假判断与应用为载体,考查了四种命题,方程根的存在性质及个数判断,难度中档.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
13.执行图的程序框图后,输出的结果为( )
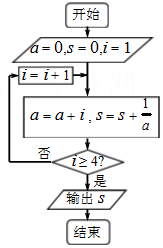

| A. | $\frac{8}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
6.已知条件p:k=$\sqrt{3}$;条件q:直线y=kx+2与圆x2+y2=1相切,则¬p是¬q的( )
| A. | 充分必要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
13.“a=-1”是“直线x+ay=1与直线ax+y=5平行”的( )条件.
| A. | 充分但不必要 | B. | 必要但不充分 | ||
| C. | 充分 | D. | 既不充分也不必要 |
3.如图所示,正方体ABCD-A′B′C′D′的棱长为1,O是平面A′B′C′D′的中心,则O到平面ABC′D′的距离是( )
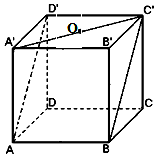

| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
8.已知sinx+cosx=$\frac{1}{5}$(0≤x<π),则tanx的值等于( )
| A. | -$\frac{3}{4}$ | B. | -$\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |