题目内容
16.已知函数f(x)=x+sinπx,则$f(\frac{1}{2017})+f(\frac{2}{2017})+f(\frac{3}{2017})+…+f(\frac{4033}{2017})$=( )| A. | 4033 | B. | -4033 | C. | 4034 | D. | -4034 |
分析 利用题意首先求解f(x)+f(2-x)的值,然后利用倒序相加求和的方法即可求得最终结果.
解答 解:结合函数的解析式可得:
f(x)+f(2-x)=x+sinπx+(2-x)+sinπ(2-x)=x+sinπx+(2-x)-sinπx=2.
设 $S=f(\frac{1}{2017})+f(\frac{2}{2017})+f(\frac{3}{2017})+…+f(\frac{4033}{2017})$,①
则:$S=f(\frac{4033}{2017})+f(\frac{4032}{2017})+f(\frac{4031}{2017})+…+f(\frac{1}{2017})$,②
①+②可得:$2S=[f(\frac{1}{2017})+f(\frac{4033}{2017})]+…+[f(\frac{4033}{2017})+f(\frac{1}{2017})]$,
即 2S=2+2+…+2=2×4033,∴S=4033,
据此可得:$f(\frac{1}{2017})+f(\frac{2}{2017})+f(\frac{3}{2017})+…+f(\frac{4033}{2017})=4033$.
故选:A.
点评 本题考查函数值的求解,倒序相加求和,诱导公式及其应用等,重点考查学生对基础概念的理解和计算能力,属于中等题.

练习册系列答案
相关题目
1.下列函数中,y的最小值为4的是( )
| A. | $y=x+\frac{4}{x},(x≠0)$ | B. | y=-x2+2x+3 | ||
| C. | $y=sinx+\frac{4}{sinx}(0<x<π)$ | D. | y=ex+4e-x |
8.下列命题正确的是( )
| A. | a>b⇒ac2>bc2 | B. | a<b<0⇒a2b>b3 | ||
| C. | $\frac{a}{b}$>1⇒a>b且b>0 | D. | a3>b3,ab>0⇒$\frac{1}{a}$<$\frac{1}{b}$ |
6.定义在R上的偶函数f(x)满足f(x+1)=-f(x),且在[-1,0]上是增函数,下面关于f(x)的判断,其中不正确的是( )
| A. | f(x)图象关于点P(1,0)对称 | B. | f(x)图象关于直线x=1对称 | ||
| C. | f(x)在[0,1]上是减函数 | D. | f(2)=f(0) |
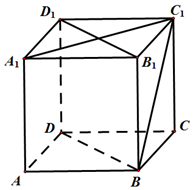 如图,已知正方体ABCD-A${\;}_{{1}_{\;}}$B1C1D1,BD,BC1,B1D1,A1C1分别为各个面的对角线;
如图,已知正方体ABCD-A${\;}_{{1}_{\;}}$B1C1D1,BD,BC1,B1D1,A1C1分别为各个面的对角线;