题目内容
6.定义在R上的偶函数f(x)满足f(x+1)=-f(x),且在[-1,0]上是增函数,下面关于f(x)的判断,其中不正确的是( )| A. | f(x)图象关于点P(1,0)对称 | B. | f(x)图象关于直线x=1对称 | ||
| C. | f(x)在[0,1]上是减函数 | D. | f(2)=f(0) |
分析 根据题意,由f(x+1)=-f(x)分析可得f(x+2)=-f(x+1)=f(x),即可得f(x)是周期为2的周期函数,可得D正确,利用函数的奇偶性分析可得函数f(x)的图象关于点P(1,0)对称,则A选项正确,B选项错误;结合周期性以及对称性分析可得C选项正确;综合即可得答案.
解答 解:根据题意,若f(x+1)=-f(x),则f(x+2)=-f(x+1)=f(x),
即f(x+2)=f(x),f(x)是周期为2的周期函数,
则有f(2)=f(0),D选项正确;
若f(x+2)=f(x),且函数f(x)为偶函数,
则有f(x+2)=f(-x),则函数f(x)的图象关于点P(1,0)对称,
则A选项正确,B选项错误;
f(x)在[-1,0]上是增函数,且函数f(x)为偶函数,
则函数f(x)在在[0,1]上是减函数,C选项正确;
故选:B
点评 本题考查抽象函数的应用,涉及函数的奇偶性以及周期性,关键是分析得到函数的周期.

练习册系列答案
相关题目
16.已知函数f(x)=x+sinπx,则$f(\frac{1}{2017})+f(\frac{2}{2017})+f(\frac{3}{2017})+…+f(\frac{4033}{2017})$=( )
| A. | 4033 | B. | -4033 | C. | 4034 | D. | -4034 |
17.已知向量$\overrightarrow a=(-1,1)$,$\overrightarrow b=(3,m)$,$\overrightarrow a∥(\overrightarrow a+\overrightarrow b)$,则m=( )
| A. | 2 | B. | -2 | C. | -3 | D. | 3 |
14.某企业为了更好地了解设备改造前后与生产合格品的关系,随机抽取了180件产品进行分析,其中设备改造前的合格品有36件,不合格品有49件,设备改造后生产的合格品有65件,不合格品有30件.根据所给数据:
(1)写出2×2列联表; (2)判断产品是否合格与设备改造是否有关,说明理由.
附:K2=$\frac{n(ad-bc)2}{(a+b)(c+d)(a+c)(b+d)}$,
数据支持:(65×49-36×30)2=4431025 101×79×85×95=64430825.
(1)写出2×2列联表; (2)判断产品是否合格与设备改造是否有关,说明理由.
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
数据支持:(65×49-36×30)2=4431025 101×79×85×95=64430825.
18.在区间[0,π]上随机地取一个x,则事件“$0≤sinx≤\frac{{\sqrt{2}}}{2}$”发生的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
15.为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间x(单位:小时)与当天投篮命中率y之间的关系:
小李这5天的平均投篮命中率;用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率.
附:线性回归方程$\widehaty=\widehatbx+\widehata$中系数计算公式$\widehatb=\frac{{\sum_{i=1}^n{({x_i}-\overline x)}({y_i}-\overline y)}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
| 时间x | 1 | 2 | 3 | 4 | 5 |
| 命中率y | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
附:线性回归方程$\widehaty=\widehatbx+\widehata$中系数计算公式$\widehatb=\frac{{\sum_{i=1}^n{({x_i}-\overline x)}({y_i}-\overline y)}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
16.调查在2~3级风的海上航行中71名乘客的晕船情况,在男人中有12人晕船,25人不晕船,在女人中有10人晕船,24人不晕船
(1)作出性别与晕船关系的列联表;
(2)根据此资料,能否在犯错误的概率不超过0.1的前提下认为2~3级风的海上航行中晕船与性别有关?
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(a+c)(b+c)(b+d)}$,n=a+b+c+d
(1)作出性别与晕船关系的列联表;
| 晕船 | 不晕船 | 总计 | |
| 男人 | |||
| 女人 | |||
| 总计 |
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(a+c)(b+c)(b+d)}$,n=a+b+c+d
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |

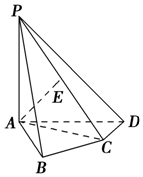 如图,在四棱锥PABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
如图,在四棱锥PABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.